Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

![]()
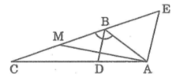
Từ (1) và (2) suy ra: BM = AB ⇒ ∆ ABM cân tại B
Tam giác cân ABM có BD là đường phân giác nên đồng thời nó cũng là đường cao (tính chất tam giác cân). Vậy BD ⊥ AM

a) Từ A kẻ AE//BD cắt đường thẳng CB tại E
=> ^BAE=^DBA=^B/2=60* và ^ABE=60* (kề bù với ^B)
=> ∆ABE đều nên AB=BE=AE=6
Do BD//AE suy ra: BD/AE=CB/CE
mà CE=CB+BE=12+6=18cm
ta có BD/6=12/18 suy ra BD=12.6/18=4 (cm)
b) Xét ∆ABM có AB=BM =6cm (do BM=MC=BC/2)
nên ∆ABM cân tại B mà BD là đường phân giác nên cũng là đường cao
do đó BD vuông góc với AM.
a) Ta có:
ˆABD=ˆCBD=ˆABC2=120∘2=60∘ABD^=CBD^=ABC^2=120∘2=60∘
Từ A kẻ đường thẳng song song với BD cắt CD tại E.
Lại có:
ˆBAE=ˆABD=60∘BAE^=ABD^=60∘ (so le trong)
ˆCBD=ˆAEB=60∘CBD^=AEB^=60∘ (đồng vị)
Suy ra tam giác ABE đều
⇒AB=BE=EA=6(cm)(1)⇒AB=BE=EA=6(cm)(1)
Khi đó: CE = BC + BE = 12 + 6 = 18 (cm)
Tam giác ACE có AE // BD nên suy ra:
BCCE=BDAE⇒BD=BC.AECE=12.618=4(cm)
b) Ta có:
MB=MC=12.BC=12.12=6(cm)(2)MB=MC=12.BC=12.12=6(cm)(2)
Từ (1) và (2) suy ra:
BM=AB⇒BM=AB⇒ ∆ABM cân tại B.
Tam giác cân ABM có BD là đường phân giác nên đồng thời nó cũng là đường cao (tính chất tam giác cân). Vậy BD⊥AM

a) Từ A kẻ AE//BD cắt đường thẳng CB tại E
=> ^BAE=^DBA=^B/2=60* và ^ABE=60* (kề bù với ^B)
=> ∆ABE đều nên AB=BE=AE=6
Do BD//AE suy ra: BD/AE=CB/CE
mà CE=CB+BE=12+6=18cm
ta có BD/6=12/18 suy ra BD=12.6/18=4 (cm)
b) Xét ∆ABM có AB=BM =6cm (do BM=MC=BC/2)
nên ∆ABM cân tại B mà BD là đường phân giác nên cũng là đường cao
do đó BD vuông góc với AM.

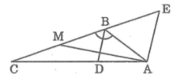

Suy ra tam giác ABE đều ⇒ AB = BE = EA = 6 (cm) (1)
Khi đó: CE = BC + BE = 12 + 6 = 18 (cm)
Tam giác ACE có AE // BD nên suy ra:
![]()
a) Ta có:
ˆABD=ˆCBD=\(\frac{\widehat{ABC}}{2}\)=120∘: 2=60∘
Từ A kẻ đường thẳng song song với BD cắt CD tại E.
Lại có:
ˆBAE=ˆABD=60∘(so le trong)
ˆCBD=ˆAEB=60∘ (đồng vị)
Suy ra tam giác ABE đều
⇒AB=BE=EA=6(cm)(1)
Khi đó: CE = BC + BE = 12 + 6 = 18 (cm)
Tam giác ACE có AE // BD nên suy ra:
\(\frac{BC}{CE}\)=\(\frac{DC}{AE}\)⇒BD=\(\frac{BC.AE}{CE}\)=\(\frac{12.6}{18}\)=4(cm)
b) Ta có:
MB=MC=\(\frac{1}{2}\).BC=\(\frac{1}{2}\).12=6(cm)(2)
Từ (1) và (2) suy ra:
BM=AB⇒BM=AB⇒ ∆ABM cân tại B.
Tam giác cân ABM có BD là đường phân giác nên đồng thời nó cũng là đường cao (tính chất tam giác cân). Vậy BD⊥AM
tk mik nha
a) Ta có:
\(\widehat{ABD}=\widehat{CBD}=\frac{\widehat{ABC}}{2}=\frac{120^o}{2}=60^o\)
Từ A kẻ đường thẳng song song với BD cắt CB tại E
Lại có:
\(\widehat{BAE}=\widehat{ABD}=60^o\) ( so le trong )
\(\widehat{CBD}=\widehat{AEB}=60^o\) ( đồng vị )
Suy ra tam giác ABE đều
=> AB = BE = EA = 6 ( cm ) (1)
Khi đó: CE = BC + BE = 12 + 6 = 18 ( cm )
Tam giác ACE có AE // BD nên suy ra :
\(\frac{BC}{CE}=\frac{BD}{AE}\)
\(\Rightarrow BD=\frac{BC.AE}{CE}=\frac{12.6}{18}=4\left(cm\right)\)
b) Ta có:
\(MB=MC=\frac{1}{2}.BC=\frac{1}{2}.12=6\left(cm\right)\left(2\right)\)
Từ (1) và (2) suy ra:
BM = AB => Tam giác ABM cân tại B.
Tam giác cân ABM có BD là đường phân giác nên đồng thời nó cũng là đường cao ( tính chất tam giác cân )
Vậy \(BD\perp AM\)