Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

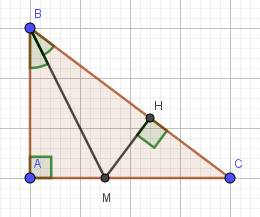
a) Xét hai tam giác vuông: \(\Delta AMB\) và \(\Delta HMB\) có:
BM là cạnh chung
\(\widehat{ABM}=\widehat{HBM}\) (do BM là phân giác của \(\widehat{ABC}\))
\(\Rightarrow\Delta AMB=\Delta HMB\) (cạnh huyền-góc nhọn)
b) Do \(\Delta AMB=\Delta HMB\) (cmt)
\(\Rightarrow AM=HM\) (hai cạnh tương ứng)
c) \(\Delta MHC\) vuông tại H
\(\Rightarrow MC\) là cạnh huyền nên là cạnh lớn nhất
\(\Rightarrow HM< MC\)
Lại có HM = AM (cmt)
\(\Rightarrow AM< MC\)

a: Xét ΔBAH vuông tại A và ΔBMH vuông tại M có
BH chung
góc ABH=góc MBH
=>ΔBAH=ΔBMH
b: BA=BM
HA=HM
=>BH là trung trực của AM
=>BH vuông góc AM
c: Xét ΔBMN vuông tại M và ΔBAC vuông tại A có
BM=BA
góc MBN chung
=>ΔMBN=ΔABC
=>BN=BC
Xét ΔBNC có BA/BN=BM/BC
nên AM//NC

a) tam giác ABM và tam giác HBM có:
<ABM = <HBM (p/g)
BM chung
<A = <H
=>tam giác ABM = tam giác AHM (ch-gn)
b) theo câu a => AM = HM =>BM là trung trực của AH
c) tam giác AKM và tam giác HMC có:
<AMK = <HMC ( đối đỉnh)
AM = HM ( theo câu b)
<MAK = <MHC (=90 độ)
=> tam giác AKM = tam giác HMC (cgv-gn)
=>MK = MC ( hai cạnh tương ứng)
d)...
a) Xét ΔAMB vuông tại A và ΔHMB vuông tại H có
BM chung
\(\widehat{ABM}=\widehat{HBM}\)(BM là tia phân giác của \(\widehat{ABH}\))
Do đó: ΔAMB=ΔHMB(Cạnh huyền-góc nhọn)
Suy ra: AM=HM(Hai cạnh tương ứng)