Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

AB=21/(3+4)x3=9 cm
AC=21-9=12cm
Tự kẻ hình bạn nhé =)))
Áp dụng định lí Pitago vào tam giác ABC , có
AB^2+AC^2=BC^2
=>thay số vào, tính được BC=15cm
Áp dụng hệ thức giữa cạnh và đường cao trong tg vuông, có:
AB^2=BHxBC
=>BH=81/15=5.4cm
=>CH=15-5.4=9.6cm
AH^2=BHxCH=5.4x9.6=51.84cm

Bài 1:
a: \(AB=21\cdot\dfrac{3}{7}=9\left(cm\right)\)
AC=21-9=12(cm)
=>BC=15(cm)
b: Xét ΔABC vuông tại A có AH là đường cao
nên \(AH\cdot BC=AB\cdot AC\)
hay AH=7,2(cm)
Xét ΔAHB vuông tại H có \(AB^2=AH^2+BH^2\)
hay BH=5,4(cm)
=>CH=9,6(cm)

\(\frac{AB}{AC}=\frac{5}{6}\)\(\Rightarrow\)\(\frac{AB}{5}=\frac{AC}{6}=x\) \(\left(x>0\right)\)
\(\Rightarrow\)\(AB=5x;\)\(AC=6x\)
Áp dụng hệ thức lượng ta có:
\(\frac{1}{AH^2}=\frac{1}{AB^2}+\frac{1}{AC^2}\)
\(\Leftrightarrow\)\(\frac{1}{9}=\frac{1}{25x^2}+\frac{1}{36x^2}\)
\(\Leftrightarrow\)\(\frac{61}{900x^2}=\frac{1}{9}\)
\(\Rightarrow\)\(900x^2=549\)
\(\Rightarrow\)\(x=\sqrt{\frac{549}{900}}=\frac{\sqrt{61}}{10}\)
\(\Rightarrow\)\(AB=\frac{\sqrt{61}}{2}\); \(AC=\frac{3\sqrt{61}}{5}\)
Áp dụng Pytago ta có:
\(AB^2+AC^2=BC^2\)
\(\Leftrightarrow\) \(BC=61x^2\)
\(\Leftrightarrow\)\(BC=x\sqrt{61}\)
\(\Leftrightarrow\)\(BC=\frac{\sqrt{61}}{10}.\sqrt{61}=6,1\)
p/s: bạn tham khảo nhé, do số không đẹp nên có lẽ mk tính toán sai 1 số chỗ, bạn bỏ qua và ktra nhé, sai đâu ib mk

\(\frac{AB}{AC}=\frac{5}{6}\)\(\Rightarrow\)\(\frac{AB}{5}=\frac{AC}{6}=x\) \(\left(x>0\right)\)
\(\Rightarrow\)\(AB=5x;\)\(AC=6x\)
Áp dụng định lý Pytago ta có:
\(AB^2+AC^2=BC^2\)
\(\Leftrightarrow\)\(BC^2=61x^2\)
\(\Leftrightarrow\)\(BC=x\sqrt{61}\)
Áp dụng hệ thức lượng ta có:
\(AB.AC=AH.BC\)
\(\Leftrightarrow\)\(30x^2=3x\sqrt{61}\)
\(\Leftrightarrow\)\(x=\frac{\sqrt{61}}{10}\)
Đến đây bạn thay x vào các biểu thức tính AB,AC,BC ở trên nhé

Ta có: \(AB^2\) = BH . BC ; \(AC^2\) = CH . BC
Ta có:
⇒ BH = 49 . 1 = 49
⇒ CH = 576 . 1 = 576
a) Ta có: \(\dfrac{BH}{HC}=\left(\dfrac{AB}{AC}\right)^2\)
\(\Leftrightarrow\dfrac{BH}{HC}=\dfrac{49}{576}\)
hay \(BH=\dfrac{49}{576}HC\)
Ta có: BH+HC=BC(H nằm giữa B và C)
\(\Leftrightarrow HC\cdot\dfrac{625}{576}=625\)
hay HC=576(cm)
\(\Leftrightarrow HB=BC-BH=625-576=49\left(cm\right)\)

\(tanB=\sqrt{2}\Rightarrow\dfrac{AC}{AB}=\sqrt{2}\Rightarrow\dfrac{AC^2}{AB^2}=2\)
\(\Rightarrow\dfrac{AC^2}{AB^2}+1=3\Rightarrow\dfrac{AC^2+AB^2}{AB^2}=3\Rightarrow\dfrac{BC^2}{AB^2}=3\)
\(\Rightarrow\dfrac{AB}{BC}=\dfrac{1}{\sqrt{3}}\)
Mà \(sinC=\dfrac{AB}{BC}\Rightarrow sinC=\dfrac{1}{\sqrt{3}}\)
\(sin^2C+cos^2C=1\Rightarrow\dfrac{1}{3}+cos^2C=1\Rightarrow cosC=\dfrac{\sqrt{6}}{3}\)
\(tanC=\dfrac{sinC}{cosC}=\dfrac{\sqrt{2}}{2}\)
b.
Trong tam giác vuông ACH:
\(sinC=\dfrac{AH}{AC}\Rightarrow AC=\dfrac{AH}{sinC}=\dfrac{2\sqrt{3}}{\dfrac{1}{\sqrt{3}}}=6\left(cm\right)\)
Trong tam giác vuông ABC:
\(tanB=\dfrac{AC}{AB}\Rightarrow AB=\dfrac{AC}{tanB}=\dfrac{6}{\sqrt{2}}=3\sqrt{2}\)
Áp dụng Pitago:
\(BC=\sqrt{AB^2+AC^2}=3\sqrt{6}\left(cm\right)\)
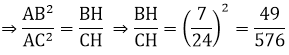
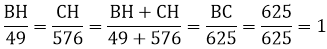
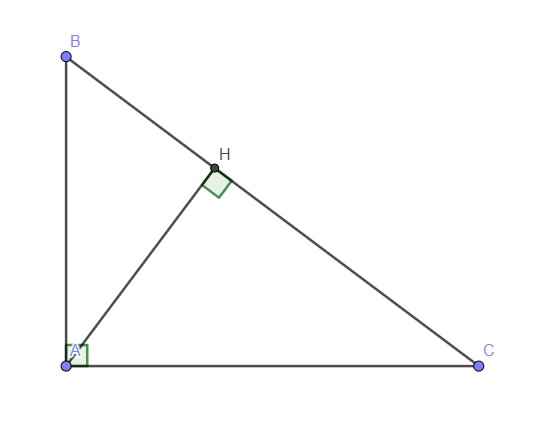
Xét ΔAHB vuông tại H có
\(AB=\dfrac{AH}{\sin30^0}=6:\dfrac{1}{2}=12\left(cm\right)\)
\(\Leftrightarrow AC=12\sqrt{3}\left(cm\right)\)
\(\Leftrightarrow BC=24\sqrt{3}\left(cm\right)\)