Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Áp dụng định lí Py ta go vào tam giác ABC có:
![]()
nên BC = 5cm
Ta có: nên AC // MN
Áp dụng định lí Ta let ta có:
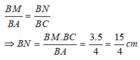
Chọn đáp án A

a,Xét tam giác ADE va tam giác ACB :
Có:AE/AB=3/9=1/3
 góc chung
AD/AC=4/12=1/3
=>tg ADE đồng dạng tg ACB(cgc)
=>AD/AC=AE/AB
b, Vì tg ADE đồng dạng tg ACB(cmt)
=> AD/AC=AE/AB=DE/CB
Mà:AD/AC=AE/AB=1/3
=>DE/CB=1/3

a) Xét ΔABC có AB=AC(gt)
nên ΔABC cân tại A(Định nghĩa tam giác cân)
Suy ra: \(\widehat{ABC}=\widehat{ACB}\)(hai góc ở đáy)
hay \(\widehat{ABH}=\widehat{ACH}\)
b) Xét ΔABH và ΔACH có
AB=AC(ΔABC cân tại A)
AH chung
BH=CH(H là trung điểm của BC)
Do đó: ΔABH=ΔACH(c-c-c)
Suy ra: \(\widehat{BAH}=\widehat{CAH}\)(hai góc tương ứng)
hay \(\widehat{MAE}=\widehat{NAE}\)
Xét ΔAME và ΔANE có
AM=AN(gt)
\(\widehat{MAE}=\widehat{NAE}\)(cmt)
AE chung
Do đó: ΔAME=ΔANE(c-g-c)
c) Ta có: ΔAME=ΔANE(cmt)
nên \(\widehat{AEM}=\widehat{AEN}\)(hai góc tương ứng)
mà \(\widehat{AEM}+\widehat{AEN}=180^0\)(hai góc so le trong)
nên \(\widehat{AEM}=\widehat{AEN}=\dfrac{180^0}{2}=90^0\)
Suy ra: AH⊥MN tại E(1)
Ta có: ΔABH=ΔACH(cmt)
nên \(\widehat{AHB}=\widehat{AHC}\)(hai góc tương ứng)
mà \(\widehat{AHB}+\widehat{AHC}=180^0\)(hai góc kề bù)
nên \(\widehat{AHB}=\widehat{AHC}=\dfrac{180^0}{2}=90^0\)
Suy ra: AH⊥BC tại H(2)
Từ (1) và (2) suy ra MN//BC(Đpcm)