Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Gọi F là trung điểm của CD
Có FE là đường trung tuyến ứng với cạnh huyền của tam giác vuông CDE
⇒FE=CF=FD=BC=CD/2
⇒ ΔCFE cân
Mà 180 độ−∠BCA=∠FCE
⇒∠FCE=60 độ
⇒ΔCFE đều
=> CF=FE=CE
Xét tam giác BFE và DCE có:
CE=FE
∠FCE=∠CFE=60 độ
BF=CD(BC=CF=FD)
⇒ Δ BFE = Δ DCE (c-g-c)
∠FBE=∠CDE=90 độ−60 độ=30 độ
=> ΔBED cân tại E
⇒BE=ED (1)
Xét Δ ABC có:
∠ABC+∠ACB+∠BAC=180 độ
⇒∠CAB=180 độ −(∠ABC+∠ACB)=180−165=15 độ
Mà ∠EBA+∠FBE=∠CBA=45 độ
⇒∠EBA=45−30=15 độ
⇒ ∠EBA=∠CAB=15 độ
⇒ ΔBEA cân tại E
=> BE=AE (2)
từ (1) và (2) => ED=AE.
=> ΔADE cân tại E
Đồng thời tam giác ADE có ∠DEA=90 độ
⇒ ΔADE là tam giác cân vuông
⇒∠EDA=∠DAE=90/2=45 độ
Mà ∠BDA=∠CDE+∠EDA=30+45=75 độ
a: Xét tứ giác ABDC có
M là trung điểm của BC
M là trung điểm của AD
Do đó: ABDC là hình bình hành
SUy ra: AB//CD
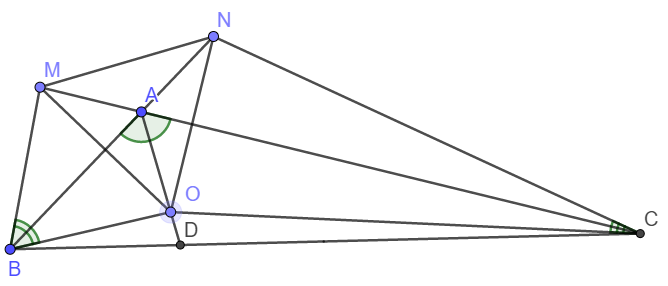
a) Xét tam giác ABC có ˆB+ˆC=60o⇒BAC=120oB^+C^=60o⇒BAC=120o
Do AD là phân giác nên ˆBAD=ˆCAD=60oBAD^=CAD^=60o
ˆMABMAB^ và ˆBACBAC^ là hai góc kề bù nên ˆMAB=180o−120o=60oMAB^=180o−120o=60o
Vậy thì ΔMAB=ΔOAB(g−c−g)ΔMAB=ΔOAB(g−c−g)
⇒AM=AO⇒AM=AO
Hoàn toàn tương tự ta có AN = AO
Vậy nên AM = AN.
b) Ta có do ΔMAB=ΔOAB⇒AM=AO;BM=BOΔMAB=ΔOAB⇒AM=AO;BM=BO
Suy ra AB là trung trực của MO,.
Lại có N thuộc AB nên NM = NO
Hoàn toàn tương tự ta có MO = MN
Vậy OM = ON = MN hay OMN là tam giác đều.
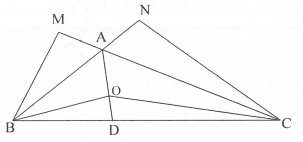Ta có: △ABC có góc B+góc C=60 độ
➩góc BAC =120 độ
ta có AD là phân giác
góc BAC=>BAD=CAD=\(\dfrac{1}{2}\)BAC=60 độ
△ABO và ΔABM có góc BAO= BAM=60 độ
AB chung
góc ABM =ABO
➩tam giác ABO =tam giác ABM (g.c.g)
➝AM=AO (*)
Ta chứng minh tương tự như trên:
tam giác ACO= tam giác ACN (g.c.g)
➝AN=AO(**)
Từ (*)(**) ⇒AM=AN (đpcm)
a: Xét ΔABH và ΔACH có
AB=AC
\(\widehat{BAH}=\widehat{CAH}\)
AH chung
Do đó: ΔABH=ΔACH
b: Xét ΔACD có AC=AD
nên ΔACD cân tại A
c: Xét ΔDCB có
CA là đường trung tuyến
CA=DB/2
Do đó:ΔDCB vuông tại C
=>DC⊥BC
mà AH⊥BC
nên DC//AH
d: ta có: DC//AH
nên \(\widehat{DCB}=90^0\)
