Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Theo hệ quả định lý Ta let ta có:
ΔABC có B’C’ // BC (B’ ∈ AB; C’ ∈ AC) ⇒ 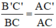
ΔAHC có H’C’ // HC (H’ ∈ AH, C’ ∈ AC) ⇒ 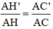
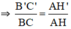
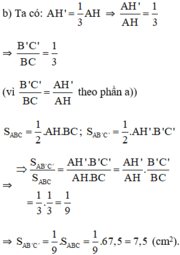

Mình cx ko bik nx tại vì này là thầy mình chụp bài của bên trường gửi qua lớp mình á, này là thầy mình gửi qua á

a, Xét \(\Delta\)HBA và \(\Delta\)ABC ta có :
\(\widehat{B}-chung\)
\(\widehat{BAC}=\widehat{BHA}\left(90^0\right)\)
\(\Rightarrow\Delta\)HBA đồng dạng với \(\Delta\)ABC(g.g)
b, Vì \(\Delta\)ABC vuông tại A => A = 90^0
Áp dụng đinh lí Py ta go ta đc :
\(BC^2=AB^2+AC^2\)
\(BC^2=12^2+16^2\)
\(BC^2=400\Leftrightarrow BC=20\)
Làm tiếp nhé.
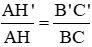 .
.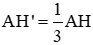 và diện tích tam giác ABC là 67,5 cm
và diện tích tam giác ABC là 67,5 cm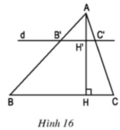
a) Chứng minh AH′AHAH′AH = B′C′BCB′C′BC
Vì B’C’ // với BC => B′C′BCB′C′BC = AB′ABAB′AB (1)
Trong ∆ABH có BH’ // BH => AH′AHAH′AH = AB′BCAB′BC (2)
Từ 1 và 2 => B′C′BCB′C′BC = AH′AHAH′AH
b) B’C’ // BC mà AH ⊥ BC nên AH’ ⊥ B’C’ hay AH’ là đường cao của tam giác AB’C’.
Áp dụng kết quả câu a) ta có: AH’ = 1313 AH
B′C′BCB′C′BC = AH′AHAH′AH = 1313 => B’C’ = 1313 BC
=> SAB’C’= 1212 AH’.B’C’ = 1212.1313AH.1313BC
=>SAB’C’= (1212AH.BC)1919
mà SABC= 1212AH.BC = 67,5 cm2
Vậy SAB’C’= 1919.67,5= 7,5 cm2