Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét tứ giác ABCD có
I là trung điểm của đường chéo AC
I là trung điểm của đường chéo BD
Do đó: ABCD là hình bình hành
b: Xét tứ giác AKCH có
I là trung điểm của đường chéo AC
I là trung điểm của đường chéo KH
Do đó: AKCH là hình bình hành
Suy ra: AK=HC

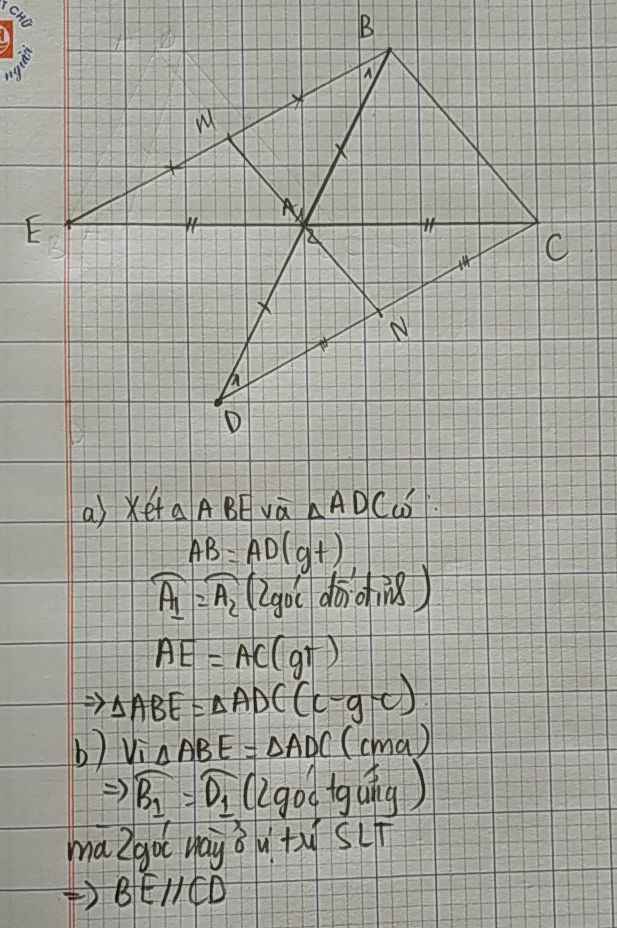
\(AD=AC\Rightarrow\)△CAD cân tại A mà AM là trung tuyến.
\(\Rightarrow\)AM cũng là đường phân giác.
\(\Rightarrow\widehat{MAE}=\dfrac{\widehat{BAE}}{2}\left(1\right)\)
\(AE=AB\Rightarrow\)△BAE cân tại A mà AN là trung tuyến.
\(\Rightarrow\)AN cũng là đường phân giác.
\(\Rightarrow\widehat{CAN}=\dfrac{\widehat{CAD}}{2}\left(2\right)\)
Ta có: \(\widehat{BAE}=\widehat{CAD}\) (đối đỉnh), nên từ (1) và (2) suy ra:
\(\widehat{EAM}=\widehat{CAN}\)
Mà \(\widehat{EAM}+\widehat{CAM}=180^0\) (kề bù)
\(\Rightarrow\widehat{CAN}+\widehat{CAM}=180^0\)
\(\Rightarrow\widehat{MAN}=180^0\)
\(\Rightarrow\)M,A,N thẳng hàng.

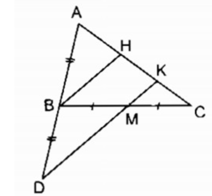
Gọi H là trung điểm của AK
Trong ∆ ADK ta có BH là đường trung bình của ∆ ADK.
⇒ BH // DK (tính chất đường trung bình của tam giác)
Hay BH // MK
Trong ∆ BCH ta có M là trung điểm của BC
MK // BH
⇒ CK = HK
AK = AH + HK = 2HK
Suy ra: AK = 2 KC ( vì HK =KC)