Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Ta cos : S tam giac ABC = 1/2 AB . AC = 1/2 . 6 . 8 = 24 cm2
S tam giacs ABC = 1/2 AH . BC = 1/2 . AH . 10 = 5AH
=> 5AH = 24
<=> AH = 4,8 cm

chứng minh rằng (1/2+1/4+1/6+...+1/2n)/(1+1/3+1/5+...1/(2n-1))
chứng minh rằng (1/2+1/4+1/6+...+1/2n)/(1+1/3+1/5+...+1/(2n-1))<n/(n+1)

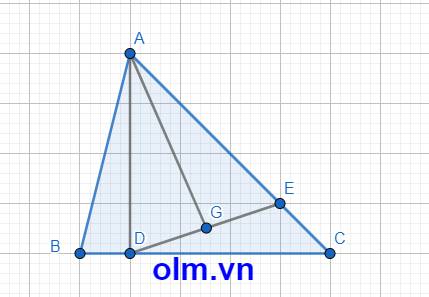
SADE = 2\(\times\)SAGE ( vì hai tam giác có chung chiều cao hạ từ đỉnh A xuống đáy DE và DE = 2\(\times\) GE )
⇒ SADE = 36 \(\times\) 2 = 72 (cm2)
SADE = \(\dfrac{3}{4}\)\(\times\)SADC (vì hai tam giác có chung chiều cao hạ từ Đỉnh D xuống đáy AC và AE = \(\dfrac{3}{4}\)AC)
⇒ SACD = 72 : \(\dfrac{3}{4}\) = 96 (cm2)
DC = BC - BD = BC - \(\dfrac{1}{5}\)BC = \(\dfrac{4}{5}\)BC
SADC = \(\dfrac{4}{5}\)SABC (vì hai tam giác có chung chiều cao hạ từ đỉnh A xuống đáy BC và DC = \(\dfrac{4}{5}\)BC)
⇒ SABC = 96 : \(\dfrac{4}{5}\) = 120 (cm2)
Tỉ số phần trăm diện tích tam giác ADE và diện tích tam giác ABC là:
72 : 120 = 0,6
0,6 = 60%
Đáp số: 60%
a, Diện tích hình tam giác là : 9 cm2
b, Tỉ số % giữa Sabe và Sabc là 67 %