Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét tứ giác BEDC có
\(\widehat{BEC}=\widehat{BDC}=90^0\)
Do đó: BEDC là tứ giác nội tiếp

a) Gọi M là trung điểm của BC.

=> ME = MB = MC = MD
Do đó bốn điểm B, E, D, C cùng thuộc đường tròn tâm M. (đpcm)
b) Trong đường tròn tâm M nói trên, ta có DE là dây, BC là đường kính nên DE < BC.

Gọi M là trung điểm của BC.

=> ME = MB = MC = MD
Do đó bốn điểm B, E, D, C cùng thuộc đường tròn tâm M. (đpcm)
a) Gọi O là trung điểm của BC ( OB = OC )
+) Xét tam giác vuông EBC ( ^BEC = 90^o )
EO là đường trung tuyến
\(\Rightarrow EO=\frac{1}{2}BC\)
\(\Rightarrow OE=OB=OC\left(1\right)\)
+) Xét tam giác vuông DBC ( ^CDB = 90^o )
DO là đường trung tuyến \(\Rightarrow DO=\frac{1}{2}BC\)
=> DO = OB = OC (2)
Từ (1)(2) => OD = OE = OB = OC
Vậy : 4 điểm B , E , D , C cùng thuộc đường tròn đường trình BC ( đpcm )

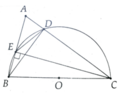
a, B,C,D,E cùng thuộc đường tròn đường kính BC
b, BC là đường kính, ED dây không qua tâm => ĐPCM

a: Xét tứ giác BCDE có
\(\widehat{BEC}=\widehat{BDC}=90^0\)
nên BCDE là tứ giác nội tiếp
hay B,C,D,E cùng thuộc một đường tròn

a) Gọi O là trung điểm của BC.
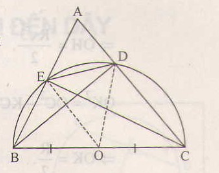
Theo tính chất trung tuyến ứng với cạnh huyền ta có:
EO=12BC;DO=12BC.EO=12BC;DO=12BC.
Suy ra OE=OD=OB=OC(=12BC)OE=OD=OB=OC(=12BC)
Do đó 4 điểm B, C, D, E cùng thuộc đường tròn (O) đường kính BC.
b) Xét đường tròn nói ở câu a), BC là đường kính, DE là một dây không qua tâm, do đó DE<BC.
a, Hai tam giác BEC và BDC vuông cùng có cạnh BC là huyền, vì vậy E,D cùng thuộc đường tròn đường kính BC, tức là điểm B,D,E,C cùng thuộc đường tròn đường kính BC
b, Xét tam giác BEC vuông tại E có BC là cạnh huyền . do đó BC>CE. Chứng minh tương tự , suy ra BC>BD