Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) tam giác ABC có BC^2=52^2=2704
mà AB^2+AC^2=20^2+48^2=2704
=> BC^2=AB^2+AC^2
=> tam giác ABC vuông tại A
b) tam giác ABC vuông tại A=> AH.BC=AB.AC
=> AH.52=20.48
=> AH.52=960
=> AH=240/13cm

sao chứng minh được \(\Delta ABC\)cân tại \(A\) khi đề bài cho \(AB=20\)và \(AC=48\)
\(\Delta\)cân là 2 cạnh bên của nó phải bằng nhau
đọc đề mình đã thấy nó không hợp lí rồi Nguyễn Hải Văn

a: Xét ΔABH vuông tại H và ΔACH vuông tại H có
AB=AC
AH chung
Do đó: ΔABH=ΔACH
Suy ra: BH=CH
b: BH=CH=6cm
=>AH=8cm
c: Xét ΔAHE có
AK là đường cao
AK là đường trung tuyến
Do đó: ΔAHE cân tại A
hay AE=AH
d: Xét ΔADH có
AI là đường cao
AI là đườngtrung tuyến
Do đó:ΔADH cân tại A
=>AD=AH=AE
=>ΔADE cân tại A

a: Xét ΔABH vuông tại H và ΔACH vuông tại H có
AB=AC
AH chung
Do đó: ΔABH=ΔAHC
Ta có: ΔABC cân tại A
mà AH là đường cao
nên AH là đường phân giác
b: Xét ΔADH vuông tại D và ΔAEH vuông tại E có
AH chung
\(\widehat{DAH}=\widehat{EAH}\)
Do đó: ΔADH=ΔAEH
Suy ra: HD=HE và AD=AE
d: Xét ΔABC có
AD/AB=AE/AC
nên DE//BC
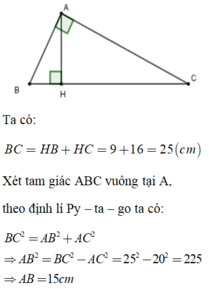

a: Xét ΔABC có \(BC^2=AB^2+AC^2\)
nên ΔABC vuông tại A
b: \(AH=\dfrac{AB\cdot AC}{BC}=\dfrac{240}{13}\left(cm\right)\)