Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

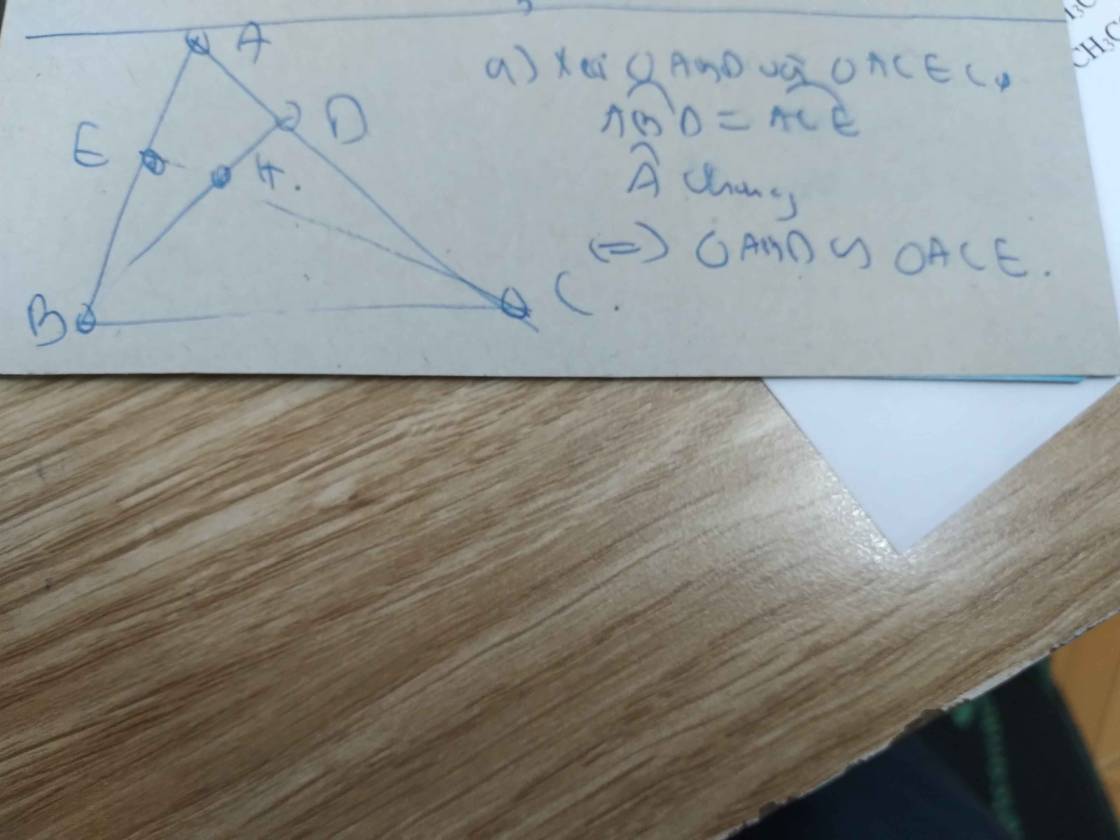
a: Xét ΔABD vuông tại D và ΔACE vuông tại E có
góc BAD chung
=>ΔABD đồng dạng với ΔACE
b: ΔABD đồng dạng với ΔACE
=>AD/AE=AB/AC
=>AD/AB=AE/AC
=>ΔADE đồng dạng với ΔABC

a: Xét ΔADB vuông tại D và ΔAEC vuông tại E có
góc A chung
=>ΔADB đồng dạng với ΔAEC
b: góc BEC=góc BDC=90 độ
=>BEDC nội tiếp
=>góc ADE=góc ABC

a: Xét ΔHEB vuông tại E và ΔHDC vuông tại D có
góc EHB=góc DHC
=>ΔHEB đồng dạng với ΔHDC
=>HE/HD=HB/HC
=>HE*HC=HB*HD
b: Xét ΔBAC có
BD,CE là đường cao
BD cắt CE tại H
=>H là trực tâm
=>AH vuông góc BC tại F
Xét ΔBFH và ΔBDC có
góc BFH=góc BDC
góc FBH chung
=>ΔBFH đồng dạng với ΔBDC
=>BF/BD=BH/BC
=>BF*BC=BD*BH

a: Xét ΔADB vuông tại D và ΔAEC vuông tại E có
góc A chung
=>ΔADB đồng dạng với ΔAEC
b: Xét ΔBKH vuông tại K và ΔBDC vuông tại D có
góc KBH chung
=>ΔBKH đồng dạng với ΔBDC
=>BK/BD=BH/BC
=>BK*BC=BD*BH

Mấy câu trên bạn lm được rồi mimhf sẽ không giải nữa mà chỉ làm câu d thôi.
Ta có : các điểm D; E; F lần lượt nằm trên các cạnh AC; AB; BC
Mà 3 đoạn thẳng AF; BD; CE đồng quy tại H
Áp dụng định lý Ceeva vào tam giác ABC ta được:
EA/EB . FB/FC . DC/DA = 1