Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

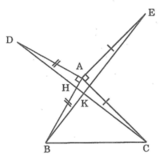
Gọi giao điểm DC và AB là H, giao điểm của CD và BE là K
Ta có: ΔABE = ΔADC (cmt)
⇒ ∠ABE = ∠ADC (hai góc t.ư)
hay ∠HBK = ∠ADH
+ ΔADH và ΔBKH đều có tổng ba góc trong mỗi tam giác bằng 180o nên có:
∠ADH + ∠DAH + ∠AHD = ∠BKH + ∠KHB + ∠HBK
Mà ∠AHD = ∠BHK (hai góc đối đỉnh)
∠ADH = ∠HBK (chứng minh trên)
Suy ra ∠DAH = ∠HKB
Mà ∠DAH = 90o nên ∠HKB = 90o
⇒ DC ⊥ BE (điều phải chứng minh)

Ta có : \(\widehat{DAB}=\widehat{CAE}=90^0\Rightarrow\widehat{DAB}+\widehat{BAC}=\widehat{CAE}+\widehat{BAC}\)
hay \(\widehat{DAC}=\widehat{EAB}\)
Xét \(\Delta ADC\)và \(\Delta ABE\)có :
AD = AB
\(\widehat{DAC}=\widehat{EAB}\)
AC = AE
\(\Rightarrow\Delta ADC=\Delta ABE\left(c.g.c\right)\Rightarrow DC=BE\)
Vì tam giác ADC = tam giác ABE nên \(\widehat{AEB}=\widehat{ACD}\)
mà \(\widehat{AKE}=\widehat{BKC}\left(doi-dinh\right),\widehat{AKE}+\widehat{AEB}=90^0\)
\(\Rightarrow\widehat{BKC}+\widehat{AEB}=90^0\) hay góc \(\widehat{BKC}+\widehat{ACD}=90^0\)
\(\Rightarrow DC\perp BE\)

Ta có: \(\widehat{DAC}=\widehat{DAB}+\widehat{BAC;}\widehat{BAE}=\widehat{EAC}+\widehat{BAC}.\)
Mà \(\widehat{DAB}=\widehat{EAC}\left(90^o\right);\widehat{BAC}chung.\)
\(\Rightarrow\) \(\widehat{DAC}=\widehat{BAE}.\)
Xét tam giác DAC và tam giác BAE:
+ AD = AB (gt).
+ AC = AE (gt).
+ \(\widehat{DAC}=\widehat{BAE}\left(cmt\right).\)
\(\Rightarrow\) Tam giác DAC = Tam giác BAE (c - g - c).
\(\Rightarrow\) DC = BE (2 cạnh tương ứng).
∠DAC = ∠DAB + ∠BAC = 90o + ∠BAC
∠BAE = ∠BAC + ∠CAE = ∠BAC + 90o
⇒ ∠DAC = ∠BAE
Xét ΔABE và ΔADC, ta có: