Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Giải
a) Xét \(\Delta BHF\) và \(\Delta CHE\) có:
\(\widehat{BHF}=\widehat{CHE}\) (vì đối đỉnh)
\(\widehat{BFH}=\widehat{CEH}=90^o\)
=> \(\Delta BHF\) \(\Delta CHE\) (g - g)
b) Xét \(\Delta ABE\) và \(\Delta ACF\) có:
\(\widehat{A}\) là góc chung
\(\widehat{AEB}=\widehat{AFC}=90^o\)
=> \(\Delta ABE\) \(\Delta ACF\) (g - g)
=> \(\frac{AB}{AC}=\frac{AE}{AF}\)
=> AF . AB = AE . AC
c) Xét \(\Delta AEF\) và \(\Delta ABC\) có:
\(\widehat{A}\) là góc chung
\(\frac{AE}{AB}=\frac{AF}{AC}\) (vì \(\Delta ABE\) \(\Delta ACF\))
=> \(\Delta AEF\) \(\Delta ABC\) (c - g - c)
d) Câu d mình không nghĩ ra. Bạn tự làm nha, chắc là xét tam giác đồng dạng rồi suy ra hai góc bằng nhau và sẽ suy ra đường phân giác đó.

a: Xet ΔAMB vuông tại M và ΔANC vuông tại N có
góc MAB chung
=>ΔAMB đồng dạng với ΔANC
=>AM/AN=AB/AC
=>AM*AC=AN*AB; AM/AB=AN/AC
b: Xet ΔAMN và ΔABC co
AM/AB=AN/AC
góc A chung
=>ΔAMN đồng dạng với ΔABC
c: góc MPH=góc ACN
góc NPH=góc ABM
góc ACN=góc ABM
=>góc MPH=góc NPH
=>PH là phân giác củagóc MPN

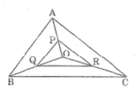
Trong △ OAB, ta có PQ là đường trung bình nên: PQ =1/2 AB (tính chất đường trung bình của tam giác)
Suy ra: 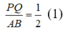 (1)
(1)
Trong △ OAC, ta có PR là đường trung bình nên:
PR = 1/2 AC (tính chất đường trung bình của tam giác)
Suy ra: 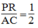 (2)
(2)
Trong △ OBC, ta có QR là đường trung bình nên
QR = 1/2 BC (tính chất đường trung bình của tam giác)
Suy ra: 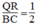
Từ (1), (2) và (3) suy ra: 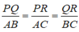
Vậy △ PQR đồng dạng △ ABC (c.c.c)


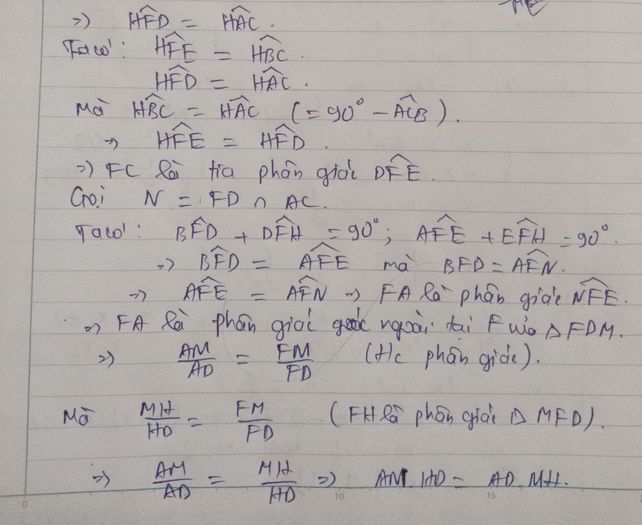 Bạn tham khảo cách làm nhé!
Bạn tham khảo cách làm nhé!