Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Xét \(\Delta ABK\)và \(\Delta C\text{D}K\)có:
\(\widehat{A_1}=\widehat{C_2}\)( 2 góc nội tiếp cùng chắn cung BD )
\(\widehat{AKB}=\widehat{CK\text{D}}\)( đối đỉnh )
\(\Rightarrow\Delta ABK~\Delta C\text{D}K\left(g-g\right)\)
\(\Rightarrow\frac{KA}{KB}=\frac{KC}{K\text{D}}\Rightarrow KA.K\text{D}=KB.KC\)
b) Kéo dài CH và BH cắt AB và AC lần lượt tại N và M
Xét \(\Delta HC\text{D}\) có:
CK vừa là đường cao vừa là đường trung tuyến
\(\Rightarrow\Delta HC\text{D}\)cân tại C
\(\Rightarrow\)CK là đường phân giác của \(\widehat{HC\text{D}}\Rightarrow\widehat{C_1}=\widehat{C_2}\)
Xét \(\Delta AMH\) và \(\Delta CKH\)có:
\(\widehat{AHM}=\widehat{CHK}\)( đối đỉnh )
\(\widehat{A_1}=\widehat{C_1}\)( cùng bằng \(\widehat{C_2}\))
\(\Rightarrow\Delta AMH~\Delta CKH\left(g-g\right)\)
\(\Rightarrow\widehat{AMH}=\widehat{CKH}=90^0\)
Hay \(CM\perp AB\)
Xét \(\Delta ABC\)có:
2 đường cao cắt nhau tại H
\(\Rightarrow\)H là trực tâm của tam giác ABC
c) Ta có: DE // BC Mà \(A\text{D}\perp BC\Rightarrow DE\perp A\text{D}\Rightarrow\widehat{FDE}=90^0\)
Xét \(\Delta AFB\)Và \(\Delta\text{E}FD\)có:
\(\widehat{F_1}=\widehat{F_2}\)( đối đỉnh )
\(\widehat{A_1}=\widehat{FED}\)( góc nội tiếp cùng chắn cung BD )
\(\Rightarrow\Delta\text{A}FB~\Delta\text{E}FD\left(g-g\right)\)
\(\Rightarrow\widehat{ABF}=\widehat{E\text{D}F}=90^0\)
Xét tam giác ABE nội tiếp đường tròn ( O, R )
có: \(\widehat{ABE}=90^0\)\(\Rightarrow\)AE là đường kính của ( O, R )
\(\Rightarrow\)A , O , E thẳng hàng

a) Vì MA là tiếp tuyến \(\Rightarrow\angle MAB=\angle MCA\) (góc tạo bởi tiếp tuyến và dây cung bằng góc nội tiếp chắn cung đó)
Xét \(\Delta MAB\) và \(\Delta MCA:\) Ta có: \(\left\{{}\begin{matrix}\angle MAB=\angle MCA\\\angle AMCchung\end{matrix}\right.\)
\(\Rightarrow\Delta MAB\sim\Delta MCA\left(g-g\right)\Rightarrow\dfrac{MA}{MC}=\dfrac{MB}{MA}\Rightarrow MA^2=MB.MC\)
b) Vì \(DE\parallel AM\) và \(AM\bot AO\) (tiếp tuyến) \(\Rightarrow DE\bot AO\)
\(\Rightarrow\angle OAD+\angle ADE=90\)
Ta có: \(\angle OAD=\dfrac{180-\angle AOC}{2}\) (\(\Delta OAC\) cân tại O) \(=90-\dfrac{1}{2}\angle AOC\)
\(=90-\angle ABC\)
\(\Rightarrow\angle ADE=\angle ABC\Rightarrow BCDE\) nội tiếp \(\Rightarrow\angle BEC=\angle BDC=90\)
\(\Rightarrow\) CE là đường cao
c) Vì N là điểm chính giữa cung BC \(\Rightarrow\angle BAN=\angle CAN\)
\(\Rightarrow AN\) là phân giác
Ta có: AI là phân giác \(\angle BAD\Rightarrow\dfrac{IB}{ID}=\dfrac{AB}{AD}\left(1\right)\)
AK là phân giác \(\angle CAE\Rightarrow\dfrac{KC}{KE}=\dfrac{AC}{AE}\left(2\right)\)
Xét \(\Delta DAB\) và \(\Delta EAC:\) Ta có: \(\left\{{}\begin{matrix}\angle AEC=\angle ADB=90\\\angle BACchung\end{matrix}\right.\)
\(\Rightarrow\Delta DAB\sim\Delta EAC\left(g-g\right)\Rightarrow\dfrac{AB}{AD}=\dfrac{AC}{AE}\left(3\right)\)
Từ (1),(2) và (3) \(\Rightarrow\dfrac{IB}{ID}=\dfrac{KC}{KE}\)
Theo đề: \(\dfrac{IB}{ID}.\dfrac{KC}{KE}=\dfrac{IB}{ID}+\dfrac{KC}{KE}\Rightarrow\left(\dfrac{AB}{AD}\right)^2=2\dfrac{AB}{AD}\Rightarrow\dfrac{AB}{AD}=2\)
\(\Rightarrow\dfrac{AD}{AB}=\dfrac{1}{2}\Rightarrow cosBAC=\dfrac{1}{2}\Rightarrow\angle BAC=60\)
Vậy tam giác ABC có \(\angle BAC=60\) thì \(\dfrac{IB}{ID}.\dfrac{KC}{KE}=\dfrac{IB}{ID}+\dfrac{KC}{KE}\)

a: Xét ΔMBA và ΔMAC có
góc MAB=góc MCA
góc M chung
=>ΔMBA đồng dạng với ΔMAC
=>MB/MA=MA/MC
=>MA^2=MB*MC
=>MC/MB=AB^2/AC^2
b: EF//AM
AM vuông góc OA
=>EF vuông góc OA
=>góc AEF+góc OAE=90 độ
=>góc AEF+(180 độ-góc AOB)/2=90 độ
=>góc AEF+90 độ-góc ACB=90 độ
=>gócAEF=góc ACB
=>góc BEF+góc BCF=180 độ
=>BEFC nội tiếp
=>góc BEC=góc BFC=90 độ
Xét ΔABC có
BF,CE là đường cao
BF căt CE tại H
=>H là trực tâm
=>AH vuông góc CB tại D

a: Xét ΔMBA và ΔMAC có
góc MAB=góc MCA
góc M chung
=>ΔMBA đồng dạng với ΔMAC
=>MB/MA=MA/MC
=>MA^2=MB*MC
=>MC/MB=AB^2/AC^2
b: EF//AM
AM vuông góc OA
=>EF vuông góc OA
=>góc AEF+góc OAE=90 độ
=>góc AEF+(180 độ-góc AOB)/2=90 độ
=>góc AEF+90 độ-góc ACB=90 độ
=>gócAEF=góc ACB
=>góc BEF+góc BCF=180 độ
=>BEFC nội tiếp
=>góc BEC=góc BFC=90 độ
Xét ΔABC có
BF,CE là đường cao
BF căt CE tại H
=>H là trực tâm
=>AH vuông góc CB tại D

a) Vẽ OM \(\perp\)BC ( M \(\in\)BC )
OM cắt DE tại N
DE// BC ( gt ) có ON \(\perp\)DE ,tứ giác BCDE là hình thang
OM \(\perp\)BC => M là trung điểm của BC
ON\(\perp\)DE => N là trung điểm của DE
MN là trục đối xứng của hình thang cân=> đpcm
d) 1)BC //DE ( dt) , AD \(\perp\)BC ( gt )
=> AD\(\perp\)DE
góc ADE = 90 độ => AE là đường kính của đường tròn ( O)
=> A,O,E thẳng hàng ( đpcm )
2) BE = CD ( BECD là hình thang cân )
AE là đường kính nên góc ABE = 90 độ
Tam giác ABE vuông tại E ,theo định lí PI-ta- go có :
AB2 + BE2 = OE2
AB2 + CD2 =( 2.R)2
AB2 + CD2 =4R2
Chứng minh tương tự ,ta có : AC2 + BD2 =4R2
Ta có : AB2 + BD2 + CD2 + AC2 = 8.R2
Câu a)
Vì DE=BC nên: sđ cung BD=sđ cung CE
\(\Rightarrow\)sđ cung BE=sđ cung CD
\(\Leftrightarrow\widehat{BCE}=\widehat{DBC}\)
Tứ giác BCED có DE//BC nên BCED là hình thang
Mà \(\widehat{BCE}=\widehat{DBC}\Rightarrowđpcm\)
Câu b)
Vì ABDC là tứ giác nội tiếp nên: \(\widehat{ABA'}=\widehat{CDA'}\)
Xét \(\Delta ABA'\)và \(\Delta CDA'\)có
+\(\widehat{ABA'}=\widehat{CDA'}\)
+\(\widehat{AA'B}=\widehat{CA'B}\)
Do đó 2 tam giác đó đồng dạng
\(\Rightarrow\frac{AA'}{A'C}=\frac{A'B}{A'D}\)\(\Rightarrowđpcm\)
Câu c)
Gọi giao BH với AC là B'
Tam giác BHD có BA' vừa là đường cao và vừa là đường trung tuyến
nên tam giác BHD cân tại B
\(\Rightarrow\widehat{BHD}=\widehat{BDA}\)
\(\Leftrightarrow\widehat{AHB'}=\widehat{BDA}\)
\(\Leftrightarrow\widehat{AHB'}+\widehat{DAC}=\widehat{BDA}+\widehat{DAC}=\widehat{BDA}+\widehat{DBC}=90^o\)
\(\Leftrightarrow BB'\perp AC\)
Tam giác ABC có H là giao 2 đường cao AA' và BB'
Vậy H là trực tâm của tam giác ABC
Câu d)
Ý 1:
Có: DE//BC mà AD vuông góc BC
Suy ra: AD vuông góc DE
nên tam giác ADE vuông tại D
Suy ra: AE là đường kình đường tròn ngoại tiếp tam giác ADE
Vậy A,O,E thẳng hàng
Ý 2:
Vì BCED là hình thang cân nên:
\(\hept{\begin{cases}BE=CD\\BD=CE\end{cases}}\)\(\Leftrightarrow\hept{\begin{cases}BE^2=CD^2\\BD^2=CE^2\end{cases}\Leftrightarrow}\hept{\begin{cases}CD^2+AB^2=BE^2+AB^2=AE^2=4R^2\\AC^2+BD^2=AC^2+CE^2=AE^2=4R^2\end{cases}}\)
Cộng lại sẽ tích đc tổng đó theo R
Hình vẽ:(không biết nó có hiện ra không nên bạn thông cảm)

Ai trả lời hộ điiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiinhanh lênnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnn

a) Ta có: DE là tiếp tuyến của (O) nên ^ODE=900 . Mà OH vuông góc BE
=> ^OHE=900 => ^ODE=^OHE.
Xét tứ giác OHDE: ^OHE=^ODE=900 => Tứ giác OHDE nội tiếp đường tròn. (đpcm).
b) Dễ thấy ^EDC=^EBD (T/c góc tạo bởi tiếp tuyến và dây cung)
=> \(\Delta\)ECD ~ \(\Delta\)EDB (g.g) => \(\frac{ED}{EB}=\frac{EC}{ED}\Rightarrow ED^2=EC.EB.\)(đpcm).
c) Tứ giác OHDE nội tiếp đường tròn (cmt) => ^OEH=^ODH.
Lại có: CI//OE => ^OEH=^ICH => ^ICH=^ODH hay ^ICH=^IDH
=> Tứ giác HICD nội tiếp đường tròn => ^HID=^HCD=^BCD
Do tứ giác ABDC nội tiếp (O) => ^BCD=^BAD.
Do đó ^HID=^BAD. Mà 2 góc bên ở vị trí đồng vị => HI//AB (đpcm).
d) Gọi giao điểm của tia CI với AB là P.
Ta thấy: Đường tròn (O) có dây cung BC và OH vuông góc BC tại H => H là trung điểm BC.
Xét \(\Delta\)BPC: H là trung điểm BC; HI//BP (HI//AB); I thuộc CP => I là trung điểm CP => IC=IP (1)
Theo hệ quả của ĐL Thales; ta có: \(\frac{IP}{DM}=\frac{AI}{AD};\frac{IC}{DN}=\frac{AD}{AI}\Rightarrow\frac{IP}{DM}=\frac{IC}{DN}\)(2)
Từ (1) và (2) => DM=DN (đpcm).
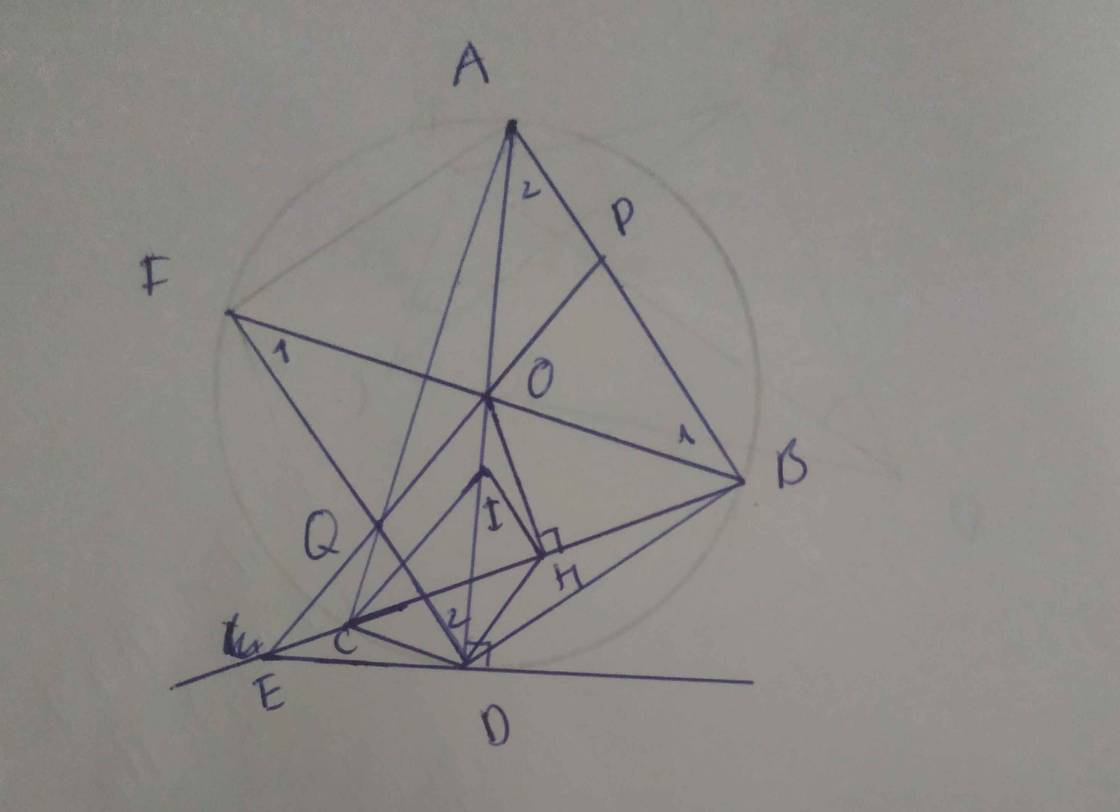

a) ta có: \(OD=OE=OA=\frac{1}{2}AE\)( bán kính đường tròn)
mà \(D\in\left(O;R\right)\)( giả thiết \(AH\)cắt \(\left(O;R\right)\)tại \(D\))
xét \(\Delta ADE\) có \(OD\) \(=\frac{1}{2}AE\)
\(\Rightarrow OD\) là đường trung tuyến ứng với cạnh \(AE\)
\(\Rightarrow\Delta ADE\) là \(\Delta\)vuông tại \(D\)
\(\Rightarrow AE\) là cạnh huyền trong tam giác vuông
ta cũng có \(O\)nằm giữa \(A,E\)( tâm đường tròn )
\(\Rightarrow A,O,E\) thẳng hàng