Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn đáp án C
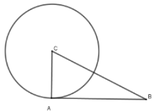
+ Xét tam giác có:
B C 2 = 5 2 = 25 ; A B 2 + A C 2 = 4 2 + 3 2 = 25 ⇒ B C 2 = A B 2 + A C 2
⇒ Δ A B C vuông tại A (Định lý Pytago đảo)
⇒ A B ⊥ A C m à A ∈ (C; CA) nên AB là tiếp tuyến của (C; CA)

c/ Nối MA; MD; ME ta có
^DME=^DMA+^CMA (1)
^DMA=90 (góc nội tiếp chắn nửa đường tròn (B)) (2)
^CMA=90 (góc nội tiếp chắn nửa đường tròn (C)) (3)
Từ (1) (2) (3) => ^DME=90 độ => D, M, E thẳng hàng

a) Xét tam giác ABC có:
\(AB^2+AC^2=8^2+6^2=100=BC^2\)
\(\Rightarrow\Delta ABC\) vuông tại A
\(\Rightarrow AB\perp AC\)
Mà \(A\in\left(C;CA\right)\)
=> AB là tiếp tuyến đường tròn (C)
b) Ta có: AB là tiếp tuyến, C là tâm
=> BC cắt đường tròn
Đáp án C
+ Xét tam giác có:
B C 2 = 5 2 = 25 ; A B 2 + A C 2 = 4 2 + 3 2 = 25 ⇒ B C 2 = A B 2 + A C 2
⇒ ΔABC vuông tại A (Định lý Pytago đảo)
⇒ AB ⊥ AC mà A ∈ (C; CA) nên AB là tiếp tuyến của (C; CA)