Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Theo định lí tổng ba góc của một tam giác bằng 180 độ: Xét trong tam giác ABC, ta có:
\(\widehat{BAC}+\widehat{ABC}+\widehat{ACB}=180^o\Rightarrow\widehat{ABC}+\widehat{ACB}=180^o-\widehat{BAC}\)(1)
Vì BI là phân giác \(\widehat{ABC}\Rightarrow\widehat{IBC}=\frac{1}{2}\widehat{ABC}\)
CI là phân giác \(\widehat{ACB}\Rightarrow\widehat{ICB}=\frac{1}{2}\widehat{ACB}\)
Xét trong tam giác ICB có: \(\widehat{BIC}+\widehat{IBC}+\widehat{ICB}=180^o\Rightarrow\widehat{BIC}=180^o-\widehat{IBC}-\widehat{ICB}=180^o-\frac{1}{2}\left(\widehat{ABC}+\widehat{ACB}\right)\)(2)
Từ (1), (2) => \(\widehat{BIC}=180^o-\frac{1}{2}\left(180^o-\widehat{BAC}\right)=90^o+\widehat{BAC}>90^o\)
=> góc BIC là góc tù cũng là góc lớn nhất=> Cạnh BC đối diện góc BIC là cạnh lớn nhất trong tam giác BIC
b) Giả sử IB<IC => \(\widehat{ICB}< \widehat{IBC}\Rightarrow\widehat{ACB}< \widehat{ABC}\Rightarrow AB< AC\)

Bài 5: Cho tam giác ABC có ba góc nhọn, AB<AC. Kẻ BD vuông góc với AC tại D, CE vuông góc với AB tại E. Gọi H là giao điểm của BD và CE. So sánh độ dài HB và HC.
Bài 6: Cho tam giác ABC có AB<AC. Tia phân giác của góc B và C cắt nhau tại I. Từ I vẽ IH vuông góc với BC. So sánh độ dài HB và HC.

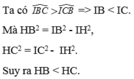
xét △ABC ta có:
AB<AC nên:\(ABC>ACB\)(do tính chát quan hệ giữa cạnh và gogs đối diện của△
\(=>\dfrac{1}{2}ABC>\dfrac{1}{2}ACB\)
\(=>IBH>ICH\)
\(=>IB< IC\)