Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

mình chỉ giúp ý d theo mong muốn của bạn thôi :)
Có : AH = AK ( cái này bạn chứng minh ở câu trên chưa mình không biết; nếu chưa thì bạn chứng minh đi nhé )
=> A thuộc đường trung trực của HK
và MH=MK
=> M thuộc đường trung trực của HK
=> AM là đường trung tực của HK
=> AM ⊥ HK

`a)`
Xét `Delta ABM` và `Delta ACM` có :
`{:(AB=AC(GT)),(AM-chung),(BM=CM(M là tđ BC)):}}`
`=>Delta ABM=Delta ACM(c.c.c)(đpcm)`
`b)`
`Delta ABM=Delta ACM(cmt)=>hat(A_1)=hat(A_2)`
mà `AM` nằm giữa `AB` và `AC`
nên `AM` là p/g của `hat(BAC)(đpcm)`
`c)`
Xét `Delta ADM` và `Delta AEM` có :
`{:(hat(ADM)=hat(AEM)(=90^)),(AM-chung),(hat(A_1)=hat(A_2)(cmt)):}}`
`=>Delta ADM=Delta AEM(ch-gn)`
`=>AD=AE` ( 2 cạnh t/ứng )
`=>Delta ADE` cân tại `A(đpcm)`

a: Xét ΔABM và ΔACM có
AM chung
AB=AC
BM=CM
Do đó: ΔABM=ΔACM
b: Ta có: ΔABC cân tại A
mà AM là đường trung tuyến
nên AM là đường cao
c: Xét tứ giác ABDC có
M là trung điểm của BC
M la trung điểm của AD
Do đó: ABDC là hình bình hành
Suy ra: AB//CD

a, Tam giác \(ABC\) cân tại \(A\)
\(\Rightarrow AB=AC;\widehat{B}=\widehat{C}\)
Xét \(\Delta ABM;\Delta ACM\) có
\(AB=AC\left(cmt\right)\\ \widehat{B}=\widehat{C}\left(cmt\right)\\ MB=MC\)
\(\Rightarrow\Delta ABM=\Delta ACM\left(c-g-c\right)\)
b, \(\Delta ABM=\Delta ACM\left(cmt\right)\)
\(\Rightarrow\widehat{HAM}=\widehat{KAM}\)
Xét \(\Delta AHM;\Delta AKM\) có
\(\widehat{HAM}=\widehat{KAM}\left(cmt\right)\\ \widehat{AHM}=\widehat{AKM}=90^o\)
\(AM\) chung
\(\Rightarrow\Delta AHM=\Delta AKM\left(ch-gn\right)\)
\(\Rightarrow HM=KM\)

a: Xét ΔABM và ΔACM có
AB=AC
AM chung
BM=CM
Do đó: ΔABM=ΔACM
b: Ta có: ΔABC cân tại A
mà AM là đường trung tuyến
nên AM là đường cao
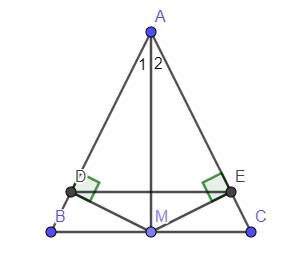
a: Xét ΔABM và ΔACM có
AB=AC
AM chung
BM=CM
Do đó: ΔABM=ΔACM