K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
15 tháng 2 2020
Bài 1.
Xét Δ ABC và Δ DEC có:
+ BC = EC (gt)
+ C1ˆ=C2ˆC1^=C2^ (đối đỉnh)
+ AC = DC (gt)
=> Δ ABC = Δ DEC (c-g-c)
=> BACˆ=EDCˆBAC^=EDC^ (2 góc tương ứng)
Mà BACˆ=90oBAC^=90o
=> EDCˆ=90o
22 tháng 12 2016
a) Vì AB // Cx nên góc ABC = BCE ( so le trong )
Xét ΔDBI và ΔECI có:
DB = EC (GT)
ABC = BCE ( chứng minh trên )
BI = CI (suy từ gt)
=> ΔDBI = ΔECI (c.g.c)
b) Do AB = AC nên ΔABC cân tại A
đc góc ABC = ACB (1)
mà AB // Cx => góc ABC = BCE (so le trong) (2)
Từ (1) và (2) suy ra ACB = BCE
Do đó CB là tia pg của góc ACE
c) Lại do ΔDBI = ΔECI nên góc BID = CIE (2 góc tương ứng)
mà 2 góc này đối nhau nên D, I, E thẳng hàng → đpcm
Chúc học tốt Tam Nguyen Thanh 
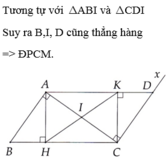
VÌ tg AID+ tg DIx=180độ
mà tg DIx+ tg EIx=180độ
suy ra tg AID= tg EIx
hay DIE= 180 độ
suy ta 3 điểm D; I:E thẳng hàng