Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
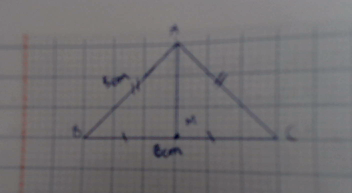cam máy tính hình nó mờ nha bạn
a) Xét ΔAMB và ΔAMC ta có:
AB=AC ( tích chất tam giác cân)
AM=MC (giả thiết)
AM cạnh chung
⇒ ΔAMB = ΔAMC (c-c-c)
⇒ \(\widehat{AMB}=\widehat{AMC}\) (hai góc tương ứng), mà hai góc này kề bù nên
\(\widehat{AMB}=\widehat{AMC}=\dfrac{180}{2}=90^o\)
Vậy AM ⊥ BC (đpcm)
b) từ câu a ta có ΔAMB = ΔAMC nên:
\(\widehat{BAM}=\widehat{CAM}\) (hai góc tương ứng)
⇒ AM là tia phân giác của \(\widehat{BAC}\) (đpcm)
c) Ta có AM ⊥ BC (1)
BM=CM (2) vì AM vuông góc với BC và M cách đều BC (BM=CM)
từ (1) và (2) ⇒ AM là đường trung trực của AB
Xét tam giác AMB và tam giác AMC có:
AB=AC(giả thiết)
AM chung
MB=MC(M là trung điểm BC)
Từ 3 điều trên, ta có tam giác AMB=tam giác AMC=>góc B=góc C
b/ Ta có tam giác AMB=tam giác AMC=>góc BAM=góc CAM=>AM là tia phân giác của góc BAC
c/ Ta có tam giác AMB=tam giác AMC=>góc AMB=góc AMC mà tổng 2 góc này bằng 180 độ=>góc AMB=góc AMC=>AM vuông góc với BC
a, Xét tam giác AMB và tam giác AMC có
AB = AC (gt)
AM chung
MB = MC ( M là trung điểm BC )
=> tam giác AMB = tam giác AMC (c.c.c)
=>\(\widehat{BAM}=\widehat{CAM}\)
=> AM là phân giác góc BAC
b, Vì tam giác AMB = tam giác AMC (cmt)
\(\Rightarrow\widehat{AMB}=\widehat{AMC}\)
Ta có : \(\widehat{AMB}+\widehat{AMC}=180^o\)(2 góc kề bù)
\(\Rightarrow\widehat{AMB}+\widehat{AMB}=180^o\)
\(\Rightarrow\widehat{AMB}=90^o\)
\(\Rightarrow AM\perp BC\left(ĐPCM\right)\)
a) Xét tam giác ABC có : AB = AC
=> Tam giác ABC cân tại A
Mà AM là đường trung tuyến ứng với BC ( vì M là trung điểm của BC)
=>AM vừa là đường trung tuyến đồng thời là đường phân giác
Do đó : AM là tia phân giác của góc BAC(đpcm)
b)Vì tam giác ABC cần tại A ( theo câu a )
Nên đường phân giác AM đồng thời là đường cao
=> AM vuông góc với BC ( đpcm )
a: Xét ΔAMB và ΔAMC có
AM chung
MB=MC
AB=AC
Do đó: ΔAMB=ΔAMC
ABM = 
c, AM vuông góc BC
a) Có: AB = AC (GT)
=> Tam giác ABC cân tại A
Xét tam giác ABM và tam giác ACM:
AB = AC (GT)
Góc B = Góc C (Tam giác ABC cân tại A)
BM = CM (GT)
=> Tam giác ABM = Tam giác ACM (c - g - c)
b) Tam giác ABM = Tam giác ACM (cmt)
=> Góc BAM = Góc CAM (2 góc tương ứng)
=> AM là phân gicacs của góc BAC
c) Tam giác ABM = Tam giác ACM (cmt)
=> Góc AMB = Góc AMC (2 góc tương ứng)
Mà 2 góc này là 2 góc kề bù
=> Góc AMB = Góc AMC = 180 độ : 2 = 90 độ
=> AM vuông góc với BC
a) Có: AB = AC (GT)
=> Tam giác ABC cân tại A
Xét tam giác ABM và tam giác ACM:
AB = AC (GT)
Góc B = Góc C (Tam giác ABC cân tại A)
BM = CM (GT)
=> Tam giác ABM = Tam giác ACM (c - g - c)
b) Tam giác ABM = Tam giác ACM (cmt)
=> Góc BAM = Góc CAM (2 góc tương ứng)
=> AM là phân gicacs của góc BAC
c) Tam giác ABM = Tam giác ACM (cmt)
=> Góc AMB = Góc AMC (2 góc tương ứng)
Mà 2 góc này là 2 góc kề bù
=> Góc AMB = Góc AMC = 180 độ : 2 = 90 độ
=> AM vuông góc với BC
a: Xét ΔABC có AB=AC
nên ΔABC cân tại A
hay \(\widehat{B}=\widehat{C}\)
