Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Áp dụng PTG: \(AB=\sqrt{BC^2-AC^2}=6\left(cm\right)\)
Áp dụng HTL:
\(\left\{{}\begin{matrix}AB^2=BH\cdot BC\\AC^2=CH\cdot BC\\AH^2=BH\cdot HC\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}BH=\dfrac{AB^2}{BC}=3,6\left(cm\right)\\CH=\dfrac{AC^2}{BC}=6,4\left(cm\right)\\AH=\sqrt{3,6\cdot6,4}=4,8\left(cm\right)\end{matrix}\right.\)
\(\sin\widehat{B}=\dfrac{AC}{BC}=\dfrac{4}{5}\approx\sin53^0\\ \Leftrightarrow\widehat{B}\approx53^0\\ \Rightarrow\widehat{C}=90^0-\widehat{B}\approx90^0-53^0=37^0\)

tam giác ABC vuông tại A nên áp dụng Py-ta-go
\(\Rightarrow BC^2=AB^2+AC^2=6^2+8^2=100\Rightarrow BC=10\left(cm\right)\)
tam giác ABC vuông tại A có đường cao AH nên áp dụng hệ thức lượng
\(\Rightarrow AB^2=BH.BC\Rightarrow BH=\dfrac{AB^2}{BC}=\dfrac{6^2}{10}=3,6\left(cm\right)\)
tam giác ABC vuông tại A có đường cao AH nên áp dụng hệ thức lượng
\(\Rightarrow AC^2=CH.BC\Rightarrow CH=\dfrac{AC^2}{BC}=\dfrac{8^2}{10}=6,4\left(cm\right)\)
tam giác ABC vuông tại A có đường cao AH nên áp dụng hệ thức lượng
\(\Rightarrow AH.BC=AB.AC\Rightarrow AH=\dfrac{AB.AC}{BC}=\dfrac{6.8}{10}=4,8\left(cm\right)\)
b) Kẻ HE,HF vuông góc với AB,AC chớ,chứ ko có điểm I
Vì \(\angle HEA=\angle HFA=\angle EAF=90\Rightarrow AEHF\) là hình chữ nhật
\(\Rightarrow EF=AH\)
tam giác AHB vuông tại H có đường cao HE nên áp dụng hệ thức lượng
\(\Rightarrow EA.EB=EH^2\)
tam giác AHB vuông tại H có đường cao HE nên áp dụng hệ thức lượng
\(\Rightarrow FA.FC=HF^2\Rightarrow EA.EB+FA.FC=EH^2+FH^2=EF^2=AH^2\)
tam giác ABC vuông tại A có đường cao AH nên áp dụng hệ thức lượng
\(\Rightarrow AH^2=HB.HC\Rightarrow HB.HC=EA.EB+FA.FC\)

Bài 5:
a) Xét ΔABC vuông tại A có
\(AC=AB\cdot\cot\widehat{C}\)
\(=21\cdot\cot40^0\)
\(\simeq25,03\left(cm\right)\)
b) Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=21^2+25,03^2=1067,5009\)
hay \(BC\simeq32,67\left(cm\right)\)

\(AC=\sqrt{BC^2-AB^2}=6\left(cm\right)\left(pytago\right)\)
Áp dụng HTL tam giác:
\(\left\{{}\begin{matrix}AB^2=BH\cdot BC\\AC^2=CH\cdot BC\\AH^2=BH\cdot HC\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}BH=\dfrac{AB^2}{BC}=6,4\left(cm\right)\\CH=\dfrac{AC^2}{BC}=3,6\left(cm\right)\\AH=\sqrt{BH\cdot HC}=4,8\left(cm\right)\end{matrix}\right.\)

\(\Delta ABC\) vuông tại A
\(\Rightarrow BC^2=AB^2+AC^2=6^2+8^2=100\)
\(\Rightarrow BC=10\left(cm\right)\)
\(\Delta ABC\) vuông tại A, đường cao AH
\(\Rightarrow AH.BC=AB.AC\) (hệ thức lượng)
\(\Rightarrow AH=\dfrac{AB.AC}{BC}=\dfrac{6.8}{10}=4,8\left(cm\right)\)
\(\Delta ABC\) vuông tại A, đường cao AH
\(\Rightarrow AB^2=BH.BC\) (hệ thức lượng)
\(\Rightarrow BH=\dfrac{AB^2}{BC}=\dfrac{6^2}{10}=3,6\left(cm\right)\)
\(\Rightarrow CH=BC-BH=10-3,6=6,4\left(cm\right)\)
Áp dụng định lý pitago vào tam giác ABC, có ah vuông góc với bc:
BC= căn của AC2 +AB2
BC= 10
Áp dụng hệ thức lượng vào tam giác ABH vuông tại H:
AB2=BC.BH
62 = 10.BH
3,6=BH
ta có: HC= 10-3,6=6,4
Áp dụng hệ thức lượng vào tam giác ABC có AH vuông BC:
AH2=BH.HC
AH2=23,04
AH= 4,8

\(a,\) Áp dụng HTL tam giác
\(\left\{{}\begin{matrix}AH^2=BH\cdot HC\\AB^2=BH\cdot BC\\AC^2=CH\cdot BC\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}CH=\dfrac{AH^2}{BH}=\dfrac{36}{4,5}=8\left(cm\right)\\AB=\sqrt{4,5\left(4,5+8\right)}=\sqrt{4,5\cdot12,5}=7,5\left(cm\right)\\AC=\sqrt{8\cdot12,5}=10\left(cm\right)\end{matrix}\right.\)
và \(BC=12,5\left(cm\right)\)
\(b,\) Áp dụng HTL tam giác
\(\left\{{}\begin{matrix}AB^2=BH\cdot BC\\AC^2=CH\cdot BC\\AH^2=CH\cdot BH\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}BC=\dfrac{AB^2}{BH}=\dfrac{36}{3}=12\left(cm\right)\\CH=\dfrac{AC^2}{BC}=\dfrac{BC^2-AB^2}{12}=\dfrac{6\sqrt{3}}{12}=\dfrac{\sqrt{3}}{2}\left(cm\right)\\AH=3\cdot\dfrac{\sqrt{3}}{2}=\dfrac{3\sqrt{3}}{2}\left(cm\right)\end{matrix}\right.\)

b) Xét tam giác ABC vuông tại A có AH là đường cao nên ta có:
A B 2 = BH.BC
⇒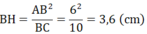
A C 2 = CH.BC
⇒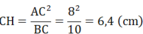
AH.BC = AB.AC
⇒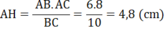
Vậy AH = 4,8 cm; BH = 3,6 cm; CH = 6,4 cm