Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

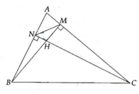
Xét tứ giác AMHN có: A M H ^ + A N H ^ = 90 0 + 90 0 = 180 0 => Đpcm
Xét tứ giác BNMC có: B N C ^ = B M C ^ = 90 0 => Đpcm


a: Xét tứ giác BNMC có
\(\widehat{BNC}=\widehat{BMC}=90^0\)
Do đó: BNMC là tứ giác nội tiếp
hay B,N,M,C cùng thuộc một đường tròn
b: Xét ΔAMB vuông tại M và ΔANC vuông tại N có
\(\widehat{NAC}\) chung
Do đó: ΔAMB\(\sim\)ΔANC
Suy ra: \(\dfrac{AM}{AN}=\dfrac{AB}{AC}\)
hay \(\dfrac{AM}{AB}=\dfrac{AN}{AC}\)
Xét ΔAMN và ΔABC có
\(\dfrac{AM}{AB}=\dfrac{AN}{AC}\)
\(\widehat{NAC}\) chung
Do đó: ΔAMN\(\sim\)ΔABC

a: góc ANH+góc AMH=180 độ
=>AMHN nội tiếp
b: Tham khảo
Tứ giác MCDE nội tiếp nên góc MED = 180 - C (1).
Tứ giác NBDE nội tiếp nên góc NED = 180 - B (2).
Mà góc MEN = 360 - MED - NED (3).
Thay (1), (2) vào (3) được: góc MEN = 360 - (180 - C) - (180 - B) = B +C = 180 - A.
Suy ra MEN + MAN =180. Vậy tứ giác MENA nội tiếp.
=>E thuộc đường tròn ngoại tiếp ΔAMN

a: Xét ΔABC có
BM là đường cao
CN là đường cao
BM cắt CN tại H
Do đó: H là trực tâm của ΔABC
=>AH\(\perp\)BC
b: Xét tứ giác AMHN có \(\widehat{AMH}+\widehat{ANH}=180^0\)
nên AMHN là tứ giác nội tiếp
c: Xét tứ giác BCMN có \(\widehat{BNC}=\widehat{BMC}=90^0\)
nên BCMN là tứ giác nội tiếp
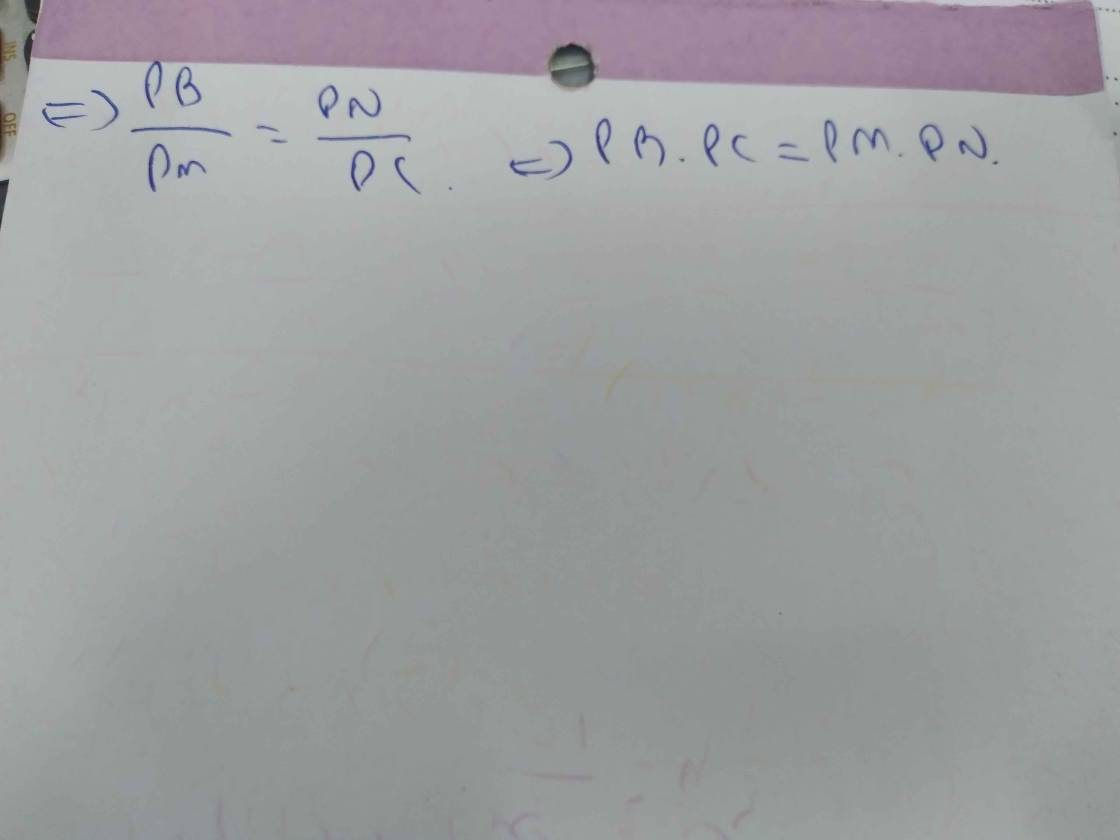
Vì BM, CN là 2 đường cao ứng vs AC, AB (gt)
\(\Rightarrow\) \(\widehat{AMB}=\widehat{ANC}\) = 90o
\(\Rightarrow\) \(\widehat{AMH}=\widehat{ANH}\) = 90o (H \(\in\) BM; H \(\in\) CN do BM \(\cap\) CN tại H)
Xét tứ giác ANHM có: \(\widehat{AMH}=\widehat{ANH}\)
\(\widehat{AMH}\) và \(\widehat{ANH}\) là 2 góc đối nhau (gt)
\(\Rightarrow\) ANHM là tứ giác nội tiếp (dhnb tứ giác nội tiếp)
Vì BM, CN là 2 đường cao ứng vs AC, AB (gt)
\(\Rightarrow\) \(\widehat{BNC}=\widehat{CMB}\) = 90o
Mà \(\widehat{BNC}\) và \(\widehat{CMB}\) đều nhìn cạnh BC với một góc 90o (cmt)
\(\Rightarrow\) BNMC là tứ giác nột tiếp (dhnb tứ giác nội tiếp)
Chúc bn học tốt!
Gọi O là trung điểm của AH
Ta có: ΔANH vuông tại N(HN⊥AB tại N)
mà NO là đường trung tuyến ứng với cạnh huyền AH(O là trung điểm của AH)
nên \(NO=\dfrac{AH}{2}\)(Định lí 1 về áp dụng hình chữ nhật vào tam giác vuông)(1)
Ta có: ΔAMH vuông tại M(HM⊥AC tại M)
mà MO là đường trung tuyến ứng với cạnh huyền AH(O là trung điểm của AH)
nên \(MO=\dfrac{AH}{2}\)(Định lí 1 về áp dụng hình chữ nhật vào tam giác vuông)(2)
Ta có: O là trung điểm của AH(cmt)
nên \(AO=OH=\dfrac{AH}{2}\)(3)
Từ (1), (2) và (3) suy ra OA=ON=OM=OH
⇔A,H,M,N∈(O)
hay tứ giác AMHN nội tiếp đường tròn(O)
Gọi D là trung điểm của BC
Ta có: ΔCBN vuông tại N(CN⊥AB tại N)
mà ND là đường trung tuyến ứng với cạnh huyền BC(D là trung điểm của BC)
nên \(ND=\dfrac{BC}{2}\)(Định lí 1 về áp dụng hình chữ nhật vào tam giác vuông)(4)
Ta có: ΔMBC vuông tại M(MB⊥AC tại M)
mà MD là đường trung tuyến ứng với cạnh huyền BC(D là trung điểm của BC)
nên \(MD=\dfrac{BC}{2}\)(Định lí 1 về áp dụng hình chữ nhật vào tam giác vuông)(5)
Ta có: D là trung điểm của BC(theo cách gọi)
nên \(BD=DC=\dfrac{BC}{2}\)(6)
Từ (4), (5) và (6) suy ra DB=DC=DN=DM
⇔B,C,N,M∈(D)
hay tứ giác BNMC nội tiếp đường tròn(D)(đpcm)