Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét tứ giác AMCK có
I là trung điểm của AC
I là trung điểm của MK
Do đó: AMCK là hình bình hành
mà \(\widehat{AMC}=90^0\)
nên AMCK là hình chữ nhật
b: \(S_{ABC}=\dfrac{AM\cdot BC}{2}=3\cdot4=12\left(cm^2\right)\)

https://lazi.vn/edu/exercise/cho-tam-giac-abc-goi-d-e-f-theo-thu-tu-la-trung-diem-cua-ab-bc-ca-goi-m-n-p-q-theo-thu-tu-la-trung-diem
Bạn xem tại link này nhé
Học tốt!!!!!!

a) Ta có: M là trung điểm của BC(gt)
nên \(BM=CM=\dfrac{BC}{2}=\dfrac{6}{2}=3cm\)
Ta có: ΔABC cân tại A(gt)
mà AM là đường trung tuyến ứng với cạnh đáy BC(M là trung điểm của BC)
nên AM là đường cao ứng với cạnh đáy BC(Định lí tam giác cân)
\(\Rightarrow AM\perp BC\)
Áp dụng định lí Pytago vào ΔABM vuông tại M, ta được:
\(AB^2=AM^2+BM^2\)
\(\Leftrightarrow AM^2=AB^2-BM^2=5^2-3^2=16\)
hay AM=4(cm)
Xét ΔABC có AM là đường cao ứng với cạnh BC(gt)
nên \(S_{ABC}=\dfrac{AM\cdot BC}{2}=\dfrac{4\cdot6}{2}=\dfrac{24}{2}=12cm^2\)
Vậy: Diện tích tam giác ABC là 12cm2
b) Xét tứ giác AMCN có
O là trung điểm của đường chéo AC(gt)
O là trung điểm của đường chéo MN(M và N đối xứng nhau qua O)
Do đó: AMCN là hình bình hành(Dấu hiệu nhận biết hình bình hành)
Hình bình hành AMCN có \(\widehat{AMC}=90^0\)(\(AM\perp BC\))
nên AMCN là hình chữ nhật(Dấu hiệu nhận biết hình chữ nhật)
c) Hình chữ nhật AMCN trở thành hình vuông khi AM=CM
mà \(CM=\dfrac{BC}{2}\)(M là trung điểm của BC)
nên \(AM=\dfrac{BC}{2}\)
Xét ΔABC có
AM là đường trung tuyến ứng với cạnh BC(M là trung điểm của BC)
\(AM=\dfrac{BC}{2}\)(cmt)
Do đó: ΔABC vuông tại A(Định lí 2 về áp dụng hình chữ nhật vào tam giác vuông)
hay \(\widehat{BAC}=90^0\)
Vậy: Khi ΔABC có thêm điều kiện \(\widehat{BAC}=90^0\) thì AMCN là hình vuông

a: Xét tứ giác BHCD có
O là trung điểm của BC
O là trung điểm của HD
Do đó: BHCD là hình bình hành

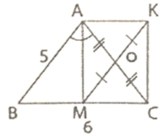
a) Vì M là trung điểm của BC nên:
BM = BC/2 = 6/2 = 3(cm)
Tam giác ABC cân tại A, lại có AM là đường phân giác nên AM cũng là đường cao. Do đó tam giác AMB vuông tại M.
Suy ra: AM2 = AB2 - BM2 (Định lí Pytago)
= 52 - 32 = 16(cm)
Suy ra AM = 4cm
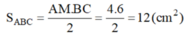
b) ΔAMC vuông tại M có MO là đường trung tuyến nên OM = OA.
Suy ra ∠OAM = ∠OMA ( ΔAMO cân tại O)
Lại có ∠OAM = ∠MAB (AM là tia phân giác góc BAC)
Suy ra ∠OMA = ∠MAB
Mà đây là 2 góc ở vị trí so le trong
Suy ra OM // AB
Vậy tứ giác ABMO là hình thang.
c) Tứ giác AMCK có OA = OC; OM = OK nên tứ giác AMCK là hình bình hành . Lại có ∠AMC = 90o (chứng minh trên) nên tứ giác AMCK là hình chữ nhật.
Hình chữ nhật AMCK là hình vuông
⇔ AM = MC = BM
⇔ AM = BC/2
⇔ ΔABC vuông cân tại A.

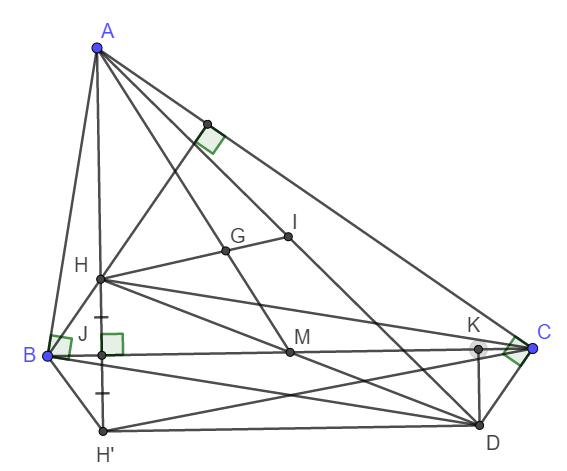
a) Ta thấy H là trực tâm tam giác ABC nên CH vuông góc AB. Suy ra DB song song CH.
Tương tự BH song song DC (Cùng vuông góc AC)
Vậy nên tứ giác BHCD là hình bình hành.
Do BHCD là hình bình hành nên \(\Delta BHC=\Delta CDB\left(c-g-c\right)\)
Lại có H' đối xứng với H qua BC nên \(\Delta BHC=\Delta BH'C\left(c-c-c\right)\)
Vậy thì \(\Delta CDB=\Delta BH'C\)
Gọi J là giao điểm của HH' và BC. Kẻ DK vuông góc BC tại K.
Khi đó ta có ngay H'J = KD. Vậy nên JKDH' là hình bình hành hay JK//H'D
Suy ra tứ giác BCDH' là hình thang.
Lại có : H'C = BD (Cùng bằng HC) nên BCDH' là hình thang cân.
b) Do BHCD là hình bình hành nên giao điểm của HD và BC là trung điểm mỗi đường. Ta gọi điểm đó là M.
Xét tam giác AHD có AM là trung tuyến, \(AG=\frac{2}{3}AM\) nên G là trọng tâm tam giác.
Vậy thì HG đi qua trung điểm AD, hay H, G, I thẳng hàng.
d) Để hình bình hành BHCD là hình thoi thì BH = HC. Vậy thì AH là đường cao đồng thời trung trực nên tam giác ABC là tam giác cân tại A.
Để hình bình hành BHCD là hình chữ nhật thì HC vuông góc BH. Lại có HC//BD nên BD//BH. Vậy thì BH trùng AB. Tương tự CH trùng AC.
Suy ra để BHCD là hình chữ nhật thì tam giác ABC vuông tại A.
SABC = \(\frac{4\times6}{2}\) = 12 (cm2)
BH là đường cao của tam giác BAC cân tại B.
=> BH là đường trung tuyến của tam giác ABC.
=> H là trung điểm của AC.
=> AH = HC = AC/2 = 6/2 = 3 (cm)
Tam giác HBC vuông tại H có:
BC2 = HB2 + HC2 (định lý Pytago)
= 42 + 32
= 16 + 9
= 25
BC = \(\sqrt{25}\) = 5 (cm)
Tam giác HBC vuông tại H có HI là đường trung tuyến (I là trung điểm của BC)
=> HI = BC/2 = 5/2 = 2,5 (cm)
I là trung điểm của BC (gt)
I là trung điểm của HD (H đối xứng D qua I)
=> BHCD là hình bình hành.
mà BHC = 900
=> BHCD là hình chữ nhật.
=> BHCD là hình vuông
<=> BH = HC
<=> Tam giác BAC có đường trung tuyến BH bằng 1 nửa cạnh AC.
<=> Tam giác ABC vuông tại B.
mà tam giác BAC cân tại B.
=> Tam giác BAC vuông cân tại B.
Vậy BHCD là hình vuông khi tam giác BAC vuông cân tại B.