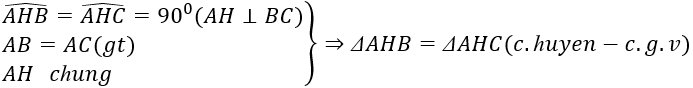Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

(Bạn tự vẽ hình giùm)
a/ \(\Delta HAB\)vuông và \(\Delta HCB\)vuông có: AB = CB (\(\Delta ABC\)cân tại A)
Cạnh HB chung
=> \(\Delta HAB\)vuông = \(\Delta HCB\)vuông (cạnh huyền - cạnh góc vuông) => HA = HC (hai cạnh tương ứng)
b/ \(\Delta AHD\)vuông và \(\Delta CHE\)vuông có: HA = HC (cm câu a)
\(\widehat{A}=\widehat{C}\)(\(\Delta ABC\)cân tại A)
=> \(\Delta AHD\)vuông = \(\Delta CHE\)vuông (cạnh huyền - góc nhọn) => HD = HE (hai cạnh tương ứng)
c/ Ta có \(\Delta AHD\)= \(\Delta CHE\)(cm câu b) => AD = CE (hai cạnh tương ứng) (1)
và AB = AC (\(\Delta ABC\)cân tại A) (2)
Lấy (2) trừ (1) => AB - AD = AC - CE
=> BD = BE => \(\Delta BDE\)cân tại B

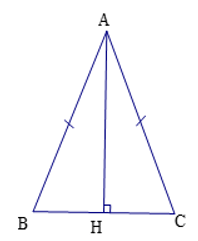
a) Xét ΔABH vuông tại H và ΔACH vuông tại H có
AB=AC(ΔABC cân tại A)
AH chung
Do đó: ΔABH=ΔACH(cạnh huyền-cạnh góc vuông)
⇔BH=CH(hai cạnh tương ứng)
b) Áp dụng định lí Pytago vào ΔABH vuông tại H, ta được:
\(BH^2+AH^2=AB^2\)
\(\Leftrightarrow BH^2=AB^2-AH^2=5^2-4^2=9\)
hay BH=3(cm)
Vậy: BH=3cm
c) Ta có: ΔABH=ΔACH(cmt)
nên \(\widehat{BAH}=\widehat{CAH}\)(hai góc tương ứng)
hay \(\widehat{DAH}=\widehat{EAH}\)
Xét ΔDAH vuông tại D và ΔEAH vuông tại E có
AH chung
\(\widehat{DAH}=\widehat{EAH}\)(cmt)
Do đó: ΔDAH=ΔEAH(cạnh huyền-góc nhọn)
Suy ra: AD=AE(hai cạnh tương ứng)
Xét ΔADE có AD=AE(cmt)
nên ΔADE cân tại A(Định nghĩa tam giác cân)

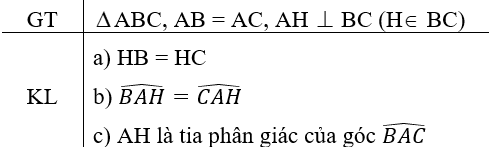
a) Chứng minh HB=HC: Xét ΔAHB và ΔAHC có: ∠AHB=∠AHC=90(độ) AH cạnh chung AB=AC(gt) ⇒ ΔAHB = ΔAHC (ch-cgv) ⇒ HB=HC (2 cạnh tương ứng)
b) Ta có: HB=HC=BC/2=6/2=3(cm) Ta có: ΔAHB vuông tại H. ⇒ AH(mũ 2)+BH(mũ 2)=AB(mũ 2) ⇒ AH(mũ 2)=AB(mũ 2)-BH(mũ 2) =4(mũ 2)-3(mũ 2)=16-9=7 ⇒ AH=√7(cm)
c) Ta có: ΔAHB = ΔAHC ⇒ ∠BAH=∠CAH Xét ΔAHD và ΔAHE có: ∠D=∠E=90(độ) AH cạnh chung ∠BAH=∠CAH (gt) ⇒ ΔAHD = ΔAHE (ch-gn) ⇒ DH=EH ⇒ ΔHDE cân tại H.

hình chắc có rồi
tam giác BEH vuông tại E => BE^2 + HE^2 = BH^2 (pytago)
HE = DH (câu b)
=> BE^2 + HD^2 = BH^2 (1)
Tam giác BHC vuông tại H => BH^2 = BC^2 - HC^2 (pytago)
HC = HA (Câu a)
=> BH^2 = HC^2 - AH^2 và (1)
=> BE^2 + DH^2 = BC^2 - AH^2
a) Xét ΔABH và ΔCBH có :
AHBˆ=CHBˆ=90o
BA = BC ( ΔABC cân ở A )
Aˆ=Cˆ ( ΔABC cân ở B )
=> ΔABH = ΔCBH ( c.h-g.n )
=> HA = HC ( 2 cạnh tương ứng )
b) Do ΔABH = ΔCBH ( c/m a )
=> ABHˆ=CBHˆ ( 2 góc tương ứng )
hay DBHˆ=EBHˆ
+) ΔBDH và ΔBEH có :
BDHˆ=BDHˆ=90o
DBHˆ=EBHˆ(cmt)
BH là cạnh chung
=> ΔBDH = ΔBEH ( c.h-g.n )
=> HE = HD ( 2 cạnh tương ứng )
c) Do ΔBDH = ΔBEH ( c/m b )
=> BD = BE ( 2 cạnh tương ứng )
=> ΔBDE cân ở B
d) Do ΔBHE vuông ở E ; áp dụng định lí Pi-ta-go , ta có :
BE2 + HE2 = BH2
Mà HE = HD (c/m b )
=> BE2 + HD2 = BH2 (*)
+) Mặt khác , ΔBCH vuông ở H , áp dụng định lí Pi-ta-go , ta có :
BC2 = BH2 + HC2
=> BC2−HC2=BH2
mà HC = HA ( c/m a )
=> BC2−HA2=BH2 (**)
Từ (*) và (**)
=> BE2+HD2=BC2−HA2(=BH2)BE2+HD2=BC2−HA2(=BH2)

a.ta có trong tam giác cân ABC đường cao cũng là đường trung tuyến => HB = HC
b.áp dụng định lý pitago ta có:
\(AB^2=AH^2+HB^2\)
\(5^2=AH^2+\left(8:2\right)^2\)
\(AH=\sqrt{5^2-4^2}=3cm\)
c.Xét tam giác vuông BHD và tam giác vuông CHE, có:
BH = CH ( cmt )
góc B = góc C ( ABC cân )
Vậy tam giác vuông BHD = tam giác vuông CHE
=> HD = HE
=> HDE cân tại H
d.ta có AB = AD + DB
AC = AE + EC
Mà BD = CE ( 2 cạnh tương ứng của 2 tam giác bằng nhau )
=> AD = AE
=> ADE cân tại A
Mà A là đường cao cũng là đường trung trực trong tam giác cân ABC cũng là đường trung trực của tam giác cân ADE ( cmx )
Chúc bạn học tốt !!!!