Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét tứ giác AIHK có
HK//AI
HI//AK
Do đó: AIHK là hình bình hành
mà \(\widehat{KAI}=90^0\)
nên AIHK là hình chữ nhật

a) B A H ^ + M A C ^ vì cùng phụ với A B C ^
b) A 1 ^ = C 1 ^ (1) (chứng minh a)
Mà DABC vuông có AM là trung tuyến nên DAMC cân tại M C 1 ^ = A 4 ^ (2).
Từ (1) và (2) suy ra A 1 ^ = A 4 ^ (3)
D thuộc đường trung trực của BC.
Þ DM ^ BC = {M}
Þ D 1 ^ = A 2 ^
Vì DM = MA (giả thiết) ⇒ M 1 ^ = A 3 ^ ⇒ A 2 ^ = A 3 ^ (4)
Từ (3) và (4) Þ AD là phân giác chung của M A H ^ & C A B ^
c) Theo cách vẽ và kết quả câu b), ta có AEDF là hình vuông.
d) DDBE = DDCF (cạnh huyền - cạnh góc vuông)
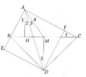

1/
Theo đề có AD//BC hay AD//BM
mà M là trung điểm BC
=>BM=4cm
Xét tứ giác ABMD có:
AD//BM và AD=BM (cmt)
vậy ABMD là hình bình hành.
b/ Áp dụng đ/l ta-lét có :
\(\dfrac{AD}{BC}=\dfrac{DE}{EB}=\dfrac{AE}{EC}=\dfrac{1}{2}\)
vậy ΔAED ∼ Δ CEB
<=> vì các cạnh của Δ AED đều = \(\dfrac{1}{2}\) cạnh của Δ CEB suy ra:
\(\dfrac{P_{AED}}{P_{CEB}}=\dfrac{1}{2}\)
https://hoc24.vn/hoi-dap/question/276790.html
Mình thấy giống bài a của bạn này á. ..... tớ nhầm D và P nhé