Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có: ΔABC cân tại A
⇒ AE là đường cao đồng thời là đường phân giác ∠BAC.
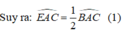
+) Tam giác ABC cân tại A nên AB = AC.
Lại có: AD = AB( giả thiết)
Suy ra: AD = AC
Do đó: ΔADC cân tại A
+) Trong tam giác ADC có: AF là đường caon nên đồng thời là đường phân giác ∠CAD.
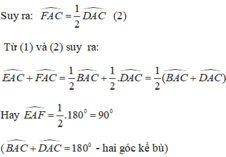

a) \(\Delta ABC\) cân tại A, AE là đường cao nên đồng thời AE là đường phân giác.
\(\Delta ACD\) cân tại A, AF là đường cao nên đồng thời là AF là đường phân giác.
AE và AF là các tia phân giác của hai góc kề bù \(\widehat{BAC},\widehat{CAD}\) nên AE \(\perp\) AF hay \(\widehat{EAF}=90^o\).

a) Xét ΔAFC vuông tại F và ΔAFD vuông tại F có
AC=AD(=AB)
AF chung
Do đó: ΔAFC=ΔAFD(Cạnh huyền-cạnh góc vuông)
Suy ra: FC=FD(hai cạnh tương ứng)
mà C,F,D thẳng hàng(gt)
nên F là trung điểm của CD
Xét ΔBCD có
CA là đường trung tuyến ứng với cạnh BD(gt)
BF là đường trung tuyến ứng với cạnh DC(cmt)
CA cắt BF tại G(gt)
Do đó: G là trọng tâm của ΔBDC(Tính chất ba đường trung tuyến của tam giác)
\(\Leftrightarrow AG=\dfrac{1}{3}AC\)(Tính chất trọng tâm của tam giác)
mà \(AC=\dfrac{1}{2}BD\left(=AB\right)\)
nên \(AG=\dfrac{1}{3}\cdot\dfrac{1}{2}BD=\dfrac{1}{6}BD\)
hay BD=6AG(đpcm)


Xét tam giác ABC cân tại A có AE là đường cao ta có:
AE đồng thời là đường phân giác của tam giác.
\(\Rightarrow\widehat{BAE}=\widehat{CAE}\)
Xét tam giác ACD cân tại A có AF là đường cao ta có:
AF đồng thời là đường phân giác của tam giác.
\(\Rightarrow\widehat{CAF}=\widehat{DAF}\)
Ta có:
\(\widehat{BAC}+\widehat{DAC}=180^o\)
\(\Rightarrow\widehat{BAE}+\widehat{CAE}+\widehat{CAF}+\widehat{DAF}=180^o\)
\(\Rightarrow2\left(\widehat{CAE}+\widehat{CAF}\right)=180^o\Rightarrow\widehat{EAF}=90^o\)
Vậy...................(đpcm)
Chúc bạn học tốt!!!

Nhớ tự vẽ hình ở nhà nhe hahaha!
a, Do BD vuông góc với AE thì ta đã biết A,D,E thẳng hàng vậy ta chỉ còn chứng minh AE=AD thì A sẽ là trung điểm của DE
Xét tam giác vuông AHC và tam giác vuông AEC, ta có
góc ACH = góc ACE (CA là tia phân giác góc BCx)
AC: cạnh chung
Do đó tam giác AHC = tam giác AEC (cạnh huyền-góc nhọn)
Suy ra AE=AH(1), góc HAC=góc CAE
Ta có góc DAB+góc BAH+góc HAC + góc CAE=180 độ mà góc BAH+HAC=90
Suy ra góc DAB+CAE=90 mà CAE =HAC (hai tam giác bằng nhau o trên)
Suy ra DAB+HAC=90 mà BAH+HAC=90
Suy ra DAB=BAH
Xét hai tam giác vuông ADB và AHB
AB cạnh chung
DAB=BAH(chung minh tren)
Do đó Hai tam giac bang nhau (cạnh huyền-góc nhọn)
Suy ra DA=AH(2)
Từ (1),(2) suy ra AD=AE
mà D,A,E thẳng hàng
Suy ra A là trung điểm của DE
b, Dùng định lý đảo của đường trung tuyến trong tam giác vuông
Ta có tam giác DHE có HA là đường trung tuyến và HA = 1/2 DE
Suy ra tam giác DHE vuông tại H(cố gắng sẽ thành công hahaha)

Tham khảo :)) 3 chữ in hoa gần nhau nghĩa là dấu góc nha :3
a, Xét ∆ABC cân tại A có AE là đường cao
=> AE đồng thời là đường pg của ∆ABC
(T/c ∆ cân)
=> AE là pg BAC
=> BAC = 2CAE (1)
Ta có AB = AC (∆ABC cân tại A) ; AB = AD (A là trđ BD)
=> AC = AD
=>∆ACD cân tại A
Mà ∆ACD có đường cao AF (gt)
=> AF là pg CAD (t/c tam giác cân)
=> CAD = 2CAF (2)
Từ (1) và (2/
=> 2(CAE + CAF) = BAC + DAC
lại có BAC + DAC = 180° (kêt bù)
=> 2(CAE + CAF) = 180°
=> 2. EAF = 180°
=> EAF = 90°
Vậy....
b, Tứ giác AECF có EAF = AEC = AFC = 90°
=> Tứ giác AECF là hcn
=> ECF = 90°
Hay BCD = 90°
Do đó ABC + BDC = 90°
Lại có ABC + EAB= 90° (∆EAB vuông tại E)
=> BDC = EAB
Hay ADF = EAB
Xét ∆BAE vuông tại E và ∆ADF vuông tại F có
BA = AD (gt)
EAB = ADF (cmt)
=>∆BAE = ∆ADF (ch-gn)
c, Ta có ∆BAE = ∆ADF (cmt)
=> ABC = DAF (2 góc t/ứ)
Mà 2 góc này ở vị trí slt
=> BC // AF
Học tốt!

gggggjjjk..hhhyh iuugln............................lklhuluiiiihhhhhhh ok-