Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

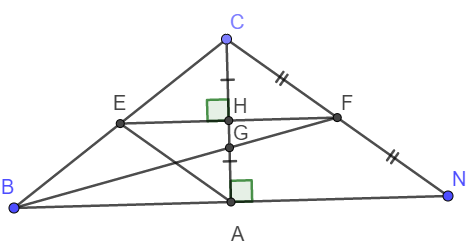
a) Áp dụng định lý Pitago trong tam giác vuông ABC, ta có:
BC2 = AC2 + AB2
252 = 152 + AB2 \(\Rightarrow ab=20\left(cm\right)\)
Xét tam giác ABC có:
AC < AB < BC nên \(\widehat{CBA}< \widehat{BCA}< \widehat{BAC}.\)
b) Xét tam giác vuông EHA và tam giác vuông EHC có:
Cạnh EH chung
HC = HA
\(\Rightarrow\Delta EHC=\Delta EHA\) (Hai cạnh góc vuông)
Do \(\Delta EHC=\Delta EHA\Rightarrow\widehat{ECA}=\widehat{EAC}\)
\(\Rightarrow\widehat{EBA}=\widehat{EAB}\) (Cùng phụ với hai góc bên trên)
Vậy nên tam giác EAB cân tại E.
c) Tam giác CBN cân tại C có CA là đường cao nên CA đồng thời là trung tuyến.
Xét tam giác CBN có CA và BF là các đường trung tuyến mà CA giao BF tại G nên G là trọng tâm tam giác.
Theo tính chất trọng tâm ta có:
\(\frac{AG}{AC}=\frac{1}{3}\Rightarrow AG=\frac{1}{5}.15=5\left(cm\right)\)
d) Xét tam giác CBN cân tại C có CA là đường cao nên đồng thời là phân giác.
Gọi giao điểm của EH với CN là F'. Khi đó ta có \(\Delta ECH=\Delta F'CH\) (Cạnh góc vuông và góc nhọn kề)
\(\Rightarrow CE=CF'\)
Lại có \(CE=\frac{1}{2}BC=\frac{1}{2}CN\Rightarrow CF'=\frac{1}{2}CN\)
Suy ra F' là trung điểm CN hay F' trùng F.
Vậy nên E, H, FA thẳng hàng.
Bài giải :

a) Áp dụng định lý Pitago trong tam giác vuông ABC, ta có:
BC2 = AC2 + AB2
252 = 152 + AB2 ⇒ab=20(cm)
Xét tam giác ABC có:
AC < AB < BC nên ^CBA<^BCA<^BAC.
b) Xét tam giác vuông EHA và tam giác vuông EHC có:
Cạnh EH chung
HC = HA
⇒ΔEHC=ΔEHA (Hai cạnh góc vuông)
Do ΔEHC=ΔEHA⇒^ECA=^EAC
⇒^EBA=^EAB (Cùng phụ với hai góc bên trên)
Vậy nên tam giác EAB cân tại E.
c) Tam giác CBN cân tại C có CA là đường cao nên CA đồng thời là trung tuyến.
Xét tam giác CBN có CA và BF là các đường trung tuyến mà CA giao BF tại G nên G là trọng tâm tam giác.
Theo tính chất trọng tâm ta có:
AGAC =13 ⇒AG=15 .15=5(cm)
d) Xét tam giác CBN cân tại C có CA là đường cao nên đồng thời là phân giác.
Gọi giao điểm của EH với CN là F'. Khi đó ta có ΔECH=ΔF'CH (Cạnh góc vuông và góc nhọn kề)
⇒CE=CF'
Lại có CE=12 BC=12 CN⇒CF'=12 CN
Suy ra F' là trung điểm CN hay F' trùng F.
Vậy nên E, H, FA thẳng hàng.

b, Cho BH = 8cm, AH = 10cm. Tính AH này là sao , biết AH mà còn bắt tính AH

Ta có CE vuông góc AB (GT)
suy ra CE là đường cao (1)
Ta có BD vuông góc AC(GT)
suy ra BD là đường cao (2)
Mà BD giao CE tại H
Từ (1) và (2) suy ra H là trực tâm (định nghĩa )
suy ra AM vuông góc BC (1)
Ta có tam giác ABC cân tại A (GT)
suy ra AB=AC (định nghĩa )
Ta có AM vuông góc BC (CMT)
suy ra góc AMB = góc AMC = 90
Xét tam giác AMB và tam giác AMC có
AM chung
góc AMB = góc AMC =90
AB= AC(CMT)
suy ra tam giác AMB = tam giác AMC (ch-cgv)
suy ra M là trung điểm BC (2)
Từ (1) và (2) suy ra AM là đường trung trực của BC
OK rồi đó

câu c nè, tam giác ahb=tam giác ahc(chứng minh trên) suy ra bh=ch(tc) suy ra dh là trung tuyến
k là trung điểm của ac(gt) suy ra ek là trung tuyến
suy ra cg cũng là trung tuyến
suy ra cg,dh,ek cùng đi qua 1 điểm

a: EC=12cm
b: Xét ΔABD vuông tại D và ΔaCE vuông tại E có
BA=CA
góc BAD chung
Do đó: ΔABD=ΔACE
Suy ra: BD=CE
c: Xét ΔIBE vuông tại E và ΔICD vuông tại D có
EB=DC
góc IBE=góc ICD
Do đó: ΔIBE=ΔICD
d: Ta có: AB=AC
nên A nằm trên đường trung trực của BC(1)
Ta co: IB=IC
nên I nằm trên đường trung trực của BC(2)
Ta có MB=MC
nen M nằm trên đường trung trực của BC(3)
Từ (1), (2) và (3) suy ra A,I,M thẳng hàng

a ) Xét ∆BAD và ∆CAD
AB = AC ( ∆ABC cân )
\(\widehat{B}=\widehat{C}\)
\(\widehat{BAD}=\widehat{DAC}\)
=> ∆ABH = ∆ACH(g.c.g)


a) Xét tam giác vuông AHB và tam giác vuông AHC có:
Cạnh AH chung
HB = HC
\(\Rightarrow\Delta AHB=\Delta AHC\) (Hai cạnh góc vuông)
b) Do HK // AB nên \(\widehat{AHK}=\widehat{BAH}\) (Hai góc so le trong)
Lại có \(\widehat{BAH}=\widehat{CAH}\)
\(\Rightarrow\widehat{KAH}=\widehat{KHA}\)
Vậy thì \(\widehat{KHC}=\widehat{KCH}\) (Cùng phụ với hai góc trên)
\(\Rightarrow\) tam giác KHC cân tại K.
c) Ta có KA = KH = KC nên K là trung điểm AC.
Vậy thì BK là trung tuyến của tam giác ABC. AH cũng là trung tuyến nên suy ra G là trọng tâm tam giác ABC.
Suy ra AG = 2/3AH = 2.6:3 = 4 (cm)
Ta có hay HK = AC/2 = AB/2 = 10:2 = 5 (cm)
d) Ta có \(2\left(AH+BK\right)=2\left(3HG+3GK\right)=6\left(HG+GK\right)\)
Xét tam giác GHK, theo bất đẳng thức tam giác ta có: HG + GK > HK
Vậy nên \(6\left(HG+GK\right)>6.HK=3.2HK=3AC\)
Tóm lại: \(2\left(AH+BK\right)>3AC\)
Bài giải :

a) Xét tam giác vuông AHB và tam giác vuông AHC có:
Cạnh AH chung
HB = HC
⇒ΔAHB=ΔAHC (Hai cạnh góc vuông)
b) Do HK // AB nên ^AHK=^BAH (Hai góc so le trong)
Lại có ^BAH=^CAH
⇒^KAH=^KHA
Vậy thì ^KHC=^KCH (Cùng phụ với hai góc trên)
⇒ tam giác KHC cân tại K.
c) Ta có KA = KH = KC nên K là trung điểm AC.
Vậy thì BK là trung tuyến của tam giác ABC. AH cũng là trung tuyến nên suy ra G là trọng tâm tam giác ABC.
Suy ra AG = 2/3AH = 2.6:3 = 4 (cm)
Ta có hay HK = AC/2 = AB/2 = 10:2 = 5 (cm)
d) Ta có 2(AH+BK)=2(3HG+3GK)=6(HG+GK)
Xét tam giác GHK, theo bất đẳng thức tam giác ta có: HG + GK > HK
Vậy nên 6(HG+GK)>6.HK=3.2HK=3AC
Tóm lại: 2(AH+BK)>3AC

bạn tự vẽ hình nhé :)
Ta có : \(\widehat{A}+\widehat{B}+\widehat{C}=180^0\)
=> B+C=180-60=120
=> 1/2B+1/2C=1/2.120=60
=> IBC+ICB=60
Ta lại có:
\(\widehat{IBC}+\widehat{ICB}+\widehat{BIC}=180^0\)
=> BIC=120
Vậy BIC=120
( bạn nhớ thêm các kí hiệu nhé )
Tự vẽ hình nha:
a) Theo định lý tổng 3 góc trong 1 \(\Delta\)ta có
\(\Delta\)ABC có :\(\widehat{CAB}+\widehat{ABC}+\widehat{ACB}\)= 1800
hay 60* + \(\widehat{ABC}+\widehat{ACB}\)=1800
\(\Rightarrow\)\(\widehat{ABC}+\widehat{ACB}\)=1800 - 600 =1200
Vì CE và BD là tia phân giác của \(\widehat{ABC}\)và \(\widehat{ACB}\)
\(\Rightarrow\)\(\widehat{DBC}+\widehat{ECB}\)= \(\frac{120^0}{2}\)=600
Theo định lý tổng 3 góc trong 1 \(\Delta\)ta có
\(\Delta CIB\)có : \(\widehat{ICB}+\widehat{IBC}+\widehat{BIC}\)=1800
hay 600 + \(\widehat{BIC}\)=1800
\(\Rightarrow\)\(\widehat{BIC}\)=1800 - 600 = 1200
a: Xét ΔABD và ΔACE có
AB=AC
góc A chung
AD=AE
Do đó: ΔABD=ΔACE
b: Xét ΔGCB có \(\widehat{GBC}=\widehat{GCB}\)
nên ΔGBC cân tại G
c: Xét ΔBAG và ΔCAG có
AB=AC
AG chung
BG=CG
DO đó: ΔBAG=ΔCAG
Suy ra: \(\widehat{BAG}=\widehat{CAG}\)
hay AG là tia phân giác của góc BAC