Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét ΔACD có \(\widehat{ACD}\) là góc tù
nên AD là cạnh lớn nhất
Suy ra: AD>AC
hay AD>AB

Xét △ BCF và △ CBE có:
\(\widehat{B}=\widehat{C}\) ( △ ABC cân tại A )
BC chung
\(\widehat{E}=\widehat{F}\left(=90^0\right)\)
⇒ △ BCF = △ CBE
⇒ BE = CF ( 2 cạnh tương ứng ) (1)
Có \(\widehat{DCF}>90^0\) ⇒ DF > CF (2)
Từ (1) và (2) ⇒ DF > BE

Bài 1:
Cm: Do Bx nằm giữa tia BA và BC nên \(\widehat{ABx}+\widehat{xBC}=\widehat{B}\)
=> \(\widehat{xBC}< \widehat{B}\) hay \(\widehat{DBC}< \widehat{B}\)(1)
D là điểm nằm ngoài t/giác ABC => tia CA nằm giữa CB và CD
=> \(\widehat{BCA}+\widehat{ACD}=\widehat{BCD}\)
=> \(\widehat{BCA}< \widehat{BCD}\) (2)
Mà \(\widehat{B}=\widehat{BCA}\) (Vì t/giác ABC cân tại A) (3)
Từ (1); (2); (3) => \(\widehat{DBC}< \widehat{BCD}\)
=> DC < BD (quan hệ giữa cạnh và góc đối diện)

1: Xét ΔCBD có CA vừa là đường cao, vừa là trung tuyến
=>ΔCBD cân tại C
=>CA là phân giác của góc BCD
2: Xét ΔCEI vuông tại E và ΔCFI vuông tại F có
CI chung
góc ECI=góc FCI
=>ΔCEI=ΔCFI
=>CE=CF
Xét ΔCBD có CE/CD=CF/CB
nên EF//BD
3: IE=IF
IF<IB
=>IE<IB

a)
+ Trong ΔABC có: góc ABC đối diện cạnh AC, góc ACB đối diện cạnh AB.
b) ΔAED có:
⇒ AE < AD hay AD > AE
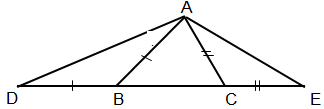

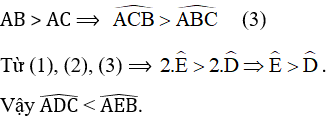

a) Vì trong một tam giác cân hai góc ở đáy không bao giờ là hai góc tù
nên \(\widehat{ACB}=\widehat{ABC}< 90^0\)
Ta có: \(\widehat{ACB}+\widehat{ACD}=180^0\)(hai góc kề bù)
mà \(\widehat{ACB}< 90^0\)(cmt)
nên \(\widehat{ACD}>90^0\)
Xét ΔACD có \(\widehat{ACD}\) tù(cmt)
mà cạnh đối diện với góc ACD là AD
nên AD là cạnh lớn nhất trong ΔACD(Trong một tam giác tù, cạnh đối diện với góc tù là cạnh lớn nhất)
hay AD>AC
mà AC=AB(ΔABC cân tại A)
nên AD>AB