Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
a)ta có AB=AC
=)TAM giác ABC cân tại A
=)Góc B2=góc C1
Lại có B1+B2=180độ(kề bù)
C1+C2=180độ(kề bù)
mà B2=C1(cmt)
=)B1=C2
Xét tam giác ABM và tam giác ACN có
BM=CN(GT)
B1=C2(CMT)
AB=AC(GT)
=)TAM giác ABM = tam giác ACN (c-g-c)
=)AM=AN(2 cạnh tương ứng )
bạn tự viết kí hiệu nhá mik ko bít cách viết
a/
Ta có
\(\widehat{ABC}=\widehat{ACB}\) (2 góc ở đáy của tg cân ABC) (1)
\(\widehat{ABM}+\widehat{ABC}=\widehat{ACN}+\widehat{ACB}=180^o\)(2)
Từ (1) và (2) \(\Rightarrow\widehat{ABM}=\widehat{ACN}\)
Xét \(\Delta ABM\) và \(\Delta ACN\) có
AB=AC (cạnh bên của tg cân ABC)
BM=CN (gt)
\(\widehat{ABM}=\widehat{ACN}\left(cmt\right)\)
\(\Rightarrow\Delta ABM=\Delta ACN\left(c.g.c\right)\Rightarrow AM=AN\Rightarrow\Delta AMN\)cân tại A
b/
Xét tg vuông BME và tg vuông CNF có
\(\widehat{ABM}=\widehat{ACN}\left(cmt\right)\Rightarrow\widehat{AMN}=\widehat{ANM}\) (2 góc ở đáy của tg cân AMN)
BM=CN (gt)
\(\Rightarrow\Delta BME=\Delta CNF\) (Hai tg vuông có cạnh huyền và một góc nhọn tương ứng = nhau thì bằng nhau)
c/
Xét tg cân AMN có AM=AN (1)
\(\Delta BME=\Delta CNF\left(cmt\right)\Rightarrow ME=NF\) (2)
Từ (1) và (2) => AM-ME=AN-NF => AE=AF
Xét tg vuông AEO và tg vuông AFO có
AE=AF (cmt)
AO chung
\(\Rightarrow\Delta AEO=\Delta AFO\) (Hai tg vuông có cạnh huyền và cạnh góc vuông tương ứng bằng nhau thì bằng nhau)
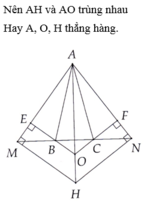
\(\Rightarrow\widehat{OAE}=\widehat{OAF}\) => AO là phân giác của \(\widehat{MAN}\)
d/
Ta có
\(\widehat{HMN}=\widehat{HMA}-\widehat{AMN}=90^o-\widehat{AMN}\)
\(\widehat{HNM}=\widehat{HNA}-\widehat{ANM}=90^o-\widehat{ANM}\)
Mà \(\widehat{AMN}=\widehat{ANM}\)
\(\Rightarrow\widehat{HMN}=\widehat{HNM}\Rightarrow\Delta HMN\) cân tại H
Ta có
\(OE\perp AM;HM\perp AM\)=> OE//HM \(\Rightarrow\widehat{AOE}=\widehat{AHM}\) (góc đồng vị)
Chứng minh tương tự ta cũng có OF//HN \(\Rightarrow\widehat{AOF}=\widehat{AHN}\) (góc đồng vị)
Mà \(\Delta AEO=\Delta AFO\Rightarrow\widehat{AOE}=\widehat{AF}\)
\(\Rightarrow\widehat{AHM}=\widehat{AHN}\)=> HO là phân giác của \(\widehat{MHN}\)
Xét tg cân HMN có
HO là phân giác của \(\widehat{MHN}\)=> HO là đường trung trực của tg HMN (trong tg cân đường phân giác của góc ở đỉnh đồng thời là đường trung trực) => \(HO\perp MN\) tại trung điểm của MN
Xét tg cân AMN có
AO là đường phân giác của \(\widehat{MAN}\) (cmt) => AO là đường trung trực của tg AMN (trong tg cân đường phân giác của góc ở đỉnh đồng thời là đường trung trực) => \(AO\perp MN\) tại trung điểm của MN
=> AO trung HO (Từ 1 điểm trên đường thẳng chỉ duy nhất dựng được 1 đường thẳng vuông góc với đường thẳng đã cho)
=> A; O; H thẳng hàng
chịu.Em mới học lơp 5 thôi anh/chị ạ.HÃy vào trang và kết bạn với em nhé
Câu a (1,0đ) Chứng minh :
ABD = 
ACE
Xét 
ABD và
ACE :có AB=AC (cạnh bên cân); 
=
(góc đáycân);BD=CE (gt) (0,25đ) x3=(0,75đ)
Vậy ABD = ACE(cgc) (0,25đ)
Câu b (0,75đ) Chứng minh đúng vuông AMD = vuông ANE vì có AD = AE; 
(do ABD =ACE) (0,5đ)
Kết luận AMD = ANE và suy ra AM =AN) (0,25đ)
Câu c (0,75đ): Chứng minh đúng vuông BMD = vuông CNE (cạnh huyền - góc nhọn )(0,25đ)
Lập luận chứng minh được 
rồi suy ra KDE cân tại K (1)(0,25đ)
Từ 
lập luận để 
(2)
Kết hợp (1)và (2) KDE đều )(0,25đ)
