Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Xét tứ giác AKCI co
M là trung điểm chung của AC và KI
nên AKCI là hình bình hành
=>CI//AK

Ta có: AN = BN = \(\dfrac{1}{2}\)AB (N là trung điểm của AB)
AM = CM = \(\dfrac{1}{2}\)AC (M là trung điểm của AC)
Mà AB = AC ( do tam giác ABC cân tại A)
=> AN = BN = AM = CM
Xét tam giác BNC và tam giác CMB:
+ BC chung
+ ^B = ^C (tam giác ABC cân tại A)
+ BN = CM (cmt)
=> Tam giác BNC = tam giác CMB (c-g-c)
=> ^NCB = ^MBC (2 góc tương ứng)
Hay ^KCB = ^KBC
=> Tam giác BKC cân tai K
Xét tam giác ABC: M là trung điểm của AC (gt)
N là trung điểm của AB (gt)
=> MN là đường trung bình của tam giác ABC (định nghĩa đường trung bình trong tam giác)
=> MN // BC (TC đường trung bình trong tam giác)
a) Ta có: \(AN=NB=\dfrac{AB}{2}\)(N là trung điểm của AB)
\(AM=MC=\dfrac{AC}{2}\)(M là trung điểm của AC)
mà AB=AC(ΔABC cân tại A)
nên AN=NB=AM=MC
Xét ΔBNC và ΔCMB có
BN=CM(cmt)
\(\widehat{NBC}=\widehat{MCB}\)(hai góc ở đáy của ΔABC cân tại A)
BC chung
Do đó: ΔBNC=ΔCMB(c-g-c)
b) Xét ΔANC và ΔABM có
AN=AM(cmt)
\(\widehat{NAC}\) chung
AC=AB(ΔABC cân tại A)
Do đó: ΔANC=ΔABM(c-g-c)
⇒\(\widehat{ACN}=\widehat{ABM}\)(hai góc tương ứng)
hay \(\widehat{NBK}=\widehat{MCK}\)
Xét ΔNBK có
\(\widehat{NBK}+\widehat{NKB}+\widehat{BNK}=180^0\)(Định lí tổng ba góc trong một tam giác)(1)
Xét ΔMCK có
\(\widehat{MCK}+\widehat{MKC}+\widehat{CMK}=180^0\)(Định lí tổng ba góc trong một tam giác)(2)
Từ (1) và (2) suy ra \(\widehat{NBK}+\widehat{NKB}+\widehat{BNK}=\widehat{MCK}+\widehat{MKC}+\widehat{CMK}\)
mà \(\widehat{NBK}=\widehat{MCK}\)(cmt)
và \(\widehat{NKB}=\widehat{MKC}\)(hai góc đối đỉnh)nên \(\widehat{BNK}=\widehat{CMK}\)Xét ΔNBK và ΔMCK có \(\widehat{BNK}=\widehat{CMK}\)(cmt)BN=CM(cmt)\(\widehat{NBK}=\widehat{MCK}\)(cmt)Do đó: ΔNBK=ΔMCK(g-c-g)⇒KB=KC(hai cạnh tương ứng)Xét ΔKBC có KB=KC(cmt)nên ΔKBC cân tại K(Định nghĩa tam giác cân)
a: Xét ΔBNC và ΔCMB có
NB=MC
\(\widehat{NBC}=\widehat{MCB}\)
BC chung
Do đó: ΔBNC=ΔCMB
b: Ta có: ΔBNC=ΔCMB
nên \(\widehat{NCB}=\widehat{MBC}\)
hay \(\widehat{KBC}=\widehat{KCB}\)
Xét ΔKBC có \(\widehat{KBC}=\widehat{KCB}\)
nên ΔKBC cân tại K
hay KB=KC

a) xét tam giác AMD và tam giác CMB có :
AM = CM ( vì Mlaf trung điểm của AC)
\(\widehat{AMD}=\widehat{CMB}\)(đối đỉnh)
MD = MB (gt)
=> tam giác AMD = tam giác CMB (c-g-c)
xét tam giác ANE và tam giác BNC có :
AN = BN ( vì N là trung điểm của AB)
\(\widehat{ANE}=\widehat{BNC}\)(đối đỉnh)
NE = CN (gt)
=> tam giác ANE = tam giác BNC (c-g-c)
b) vì tam giác AMD = tam giác CMB (cmt) => AD = BC (2 cạnh tương ứng)(1)
vì tam giác ANE = tam giác BNC (cmt) => AE = BC ( 2 cạnh tương ứng) (2)
từ (1), (2) => AD = AE (đpcm)
c) Vì tam giác AMD = tam giác CMB (cmt) => \(\widehat{MAD}=\widehat{MCB}\)(2 góc tương ứng)
mà \(\widehat{MAD}\)và \(\widehat{MCB}\)ở vị trí so le trong
do đó AD // BC (3)
Vì tam giác ANE = tam giác BNC (cmt) => \(\widehat{NAE}=\widehat{NBC}\)(2 góc tương ứng)
mà \(\widehat{NAE}\)và \(\widehat{NBC}\) ở vị trí so le trong
do đó AE // BC (4)
từ (3), (4) => A, E, D thẳng hàng (đpcm)

a)
a)Sao lại chứng minh tam giác ACD= tam giác DMA
Mà tam giác DMC<ADC(xem lại)
b)Xét tam giác DMC và tam giác BMA
MB=MD(gt)
DMC=AMB(đđ)
MA=MC(Vì M là trung điểm AC)
⇒⇒tam giác DMC=tam giác BMA(c.g.c)
⇒⇒AB=DC(cặp cạnh tương ứng)(1)
Mà AB=AC(vì tam giác ABC cân)(2)
Từ (1) và (2) suy ra:DC=AC
Vậy tam giác ACD cân tại D
c/
+ Xét tam giác BDE có
DM=BM => EM là trung tuyến thuộc cạnh BD của tg BDE (1)
+ Ta có
CA=CE (đề bài)
MA=MC (đề bài)
=> CE=2.MC hay MC=1/3ME (2)
Từ (1) và (2) =>C là trọng tâm của tam giác BDE => DC là trung tuyến thuộc cạnh BE của tg BDE => K là trung điểm của BE
MA=MC(Vì M là trung điểm AC)
$⇒⇒$⇒⇒tam giác DMC=tam giác BMA(c.g.c)
$⇒⇒$⇒⇒AB=DC(cặp cạnh tương ứng)(1)
Mà AB=AC(vì tam giác ABC cân)(2)
Từ (1) và (2) suy ra:DC=AC
Vậy tam giác ACD cân tại D
c/
+ Xét tam giác BDE có
DM=BM => EM là trung tuyến thuộc cạnh BD của tg BDE (1)
+ Ta có
CA=CE (đề bài)
MA=MC (đề bài)
=> CE=2.MC hay MC=1/3ME (2)
Từ (1) và (2) =>C là trọng tâm của tam giác BDE => DC là trung tuyến thuộc cạnh BE của tg BDE => K là trung điểm của BE
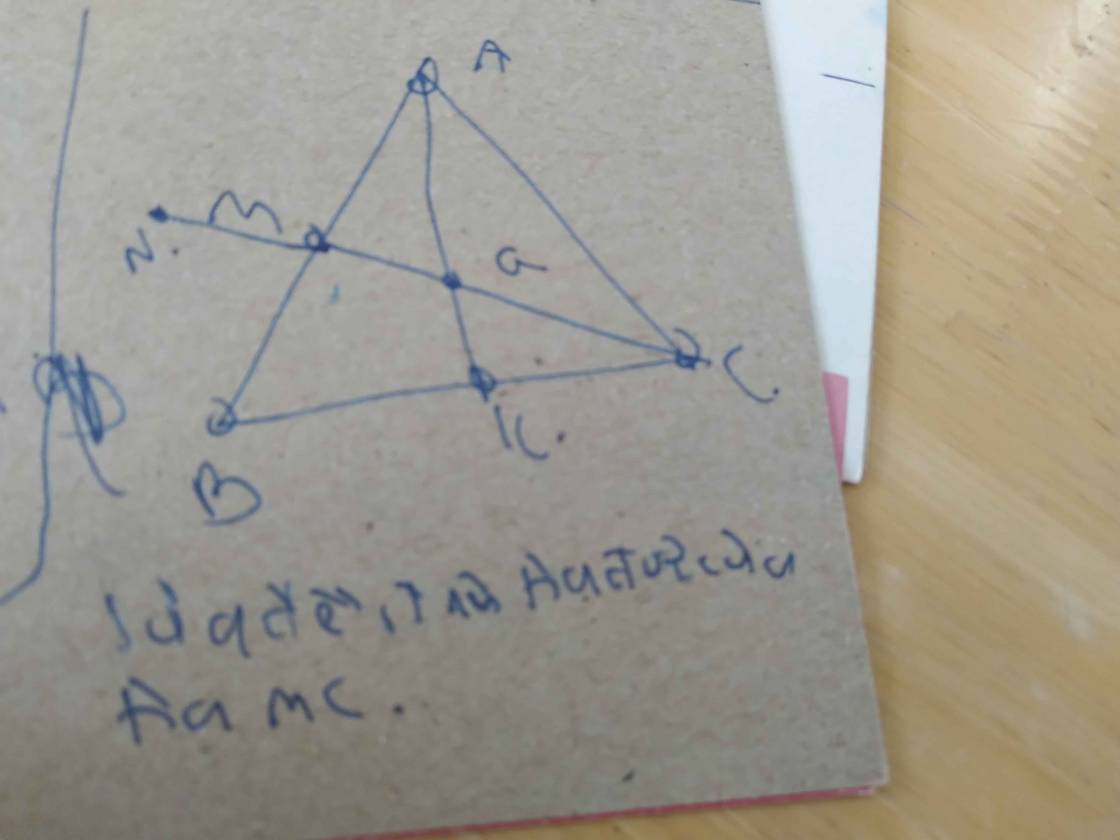


a: Xét ΔNBC và ΔMCB có
NB=MC
góc NBC=góc MCB
BC chung
=>ΔNBC=ΔMCB
b: ΔNBC=ΔMCB
=>góc KBC=góc KCB
=>ΔKBC cân tại K
c: Xét tứ giácc AKCI có
M là trung điểm chung của AC và KI
nên AKCI là hình bình hành
=>CI//AK