Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Chứng minh HB=HC: Xét ΔAHB và ΔAHC có: ∠AHB=∠AHC=90(độ) AH cạnh chung AB=AC(gt) ⇒ ΔAHB = ΔAHC (ch-cgv) ⇒ HB=HC (2 cạnh tương ứng)
b) Ta có: HB=HC=BC/2=6/2=3(cm) Ta có: ΔAHB vuông tại H. ⇒ AH(mũ 2)+BH(mũ 2)=AB(mũ 2) ⇒ AH(mũ 2)=AB(mũ 2)-BH(mũ 2) =4(mũ 2)-3(mũ 2)=16-9=7 ⇒ AH=√7(cm)
c) Ta có: ΔAHB = ΔAHC ⇒ ∠BAH=∠CAH Xét ΔAHD và ΔAHE có: ∠D=∠E=90(độ) AH cạnh chung ∠BAH=∠CAH (gt) ⇒ ΔAHD = ΔAHE (ch-gn) ⇒ DH=EH ⇒ ΔHDE cân tại H.

a: Ta có: ΔABC cân tại A
mà AH là đường cao
nên H là trung điểmcủa BC
hay HB=HC
b: Xét ΔADH vuông tạiD và ΔAEH vuông tại E có
AH chung
\(\widehat{DAH}=\widehat{EAH}\)
Do đó: ΔADH=ΔAEH
Suy ra HD=HE
hay ΔHDE cân tại H

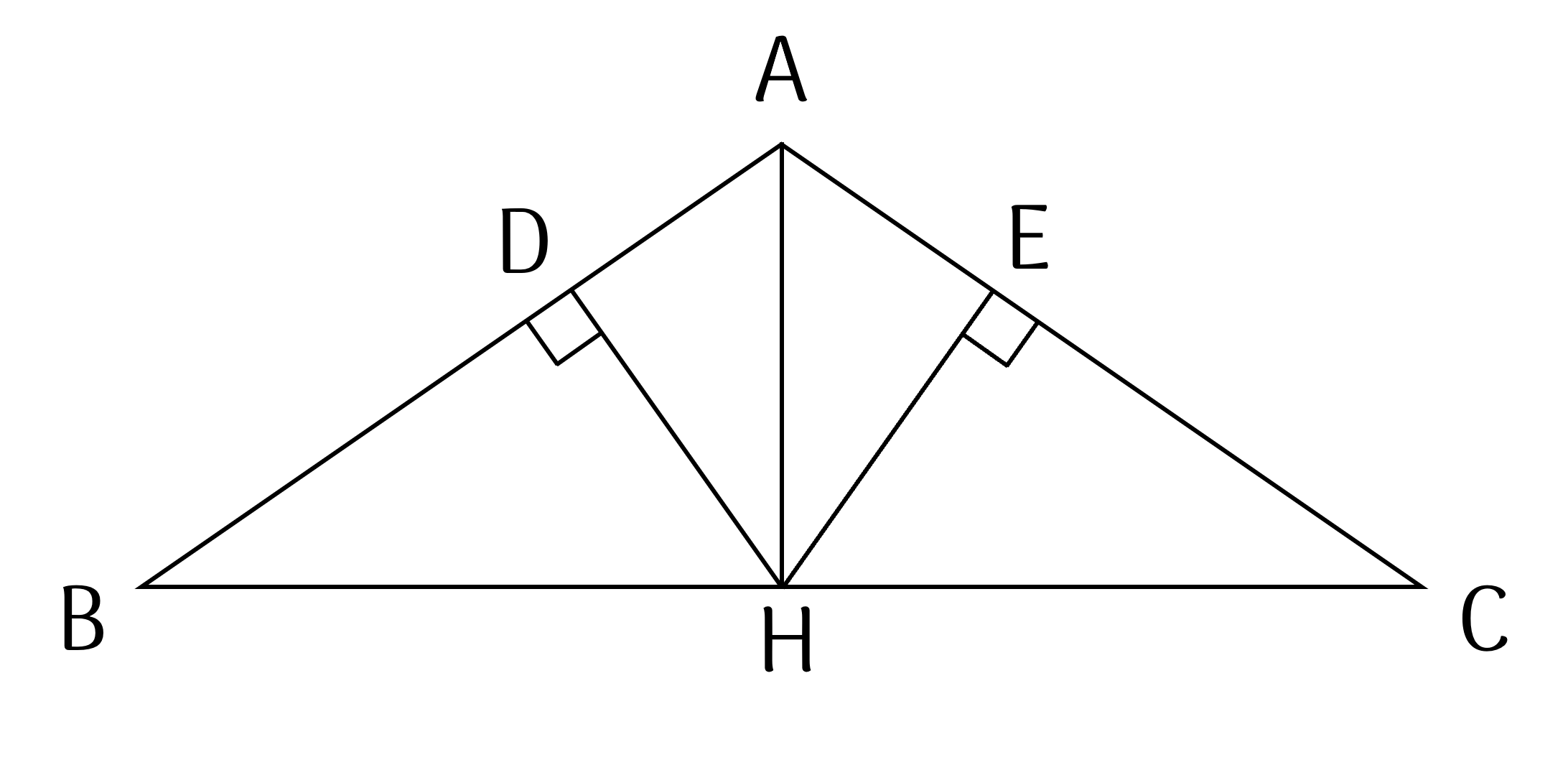
a) Xét hai tam giác vuông $AHB$ và $AHC$ có:
$AH$ là cạnh chung;
$AB = AC$ (gt);
Suy ra $\Delta AHB=\Delta AHC$ (cạnh huyền - cạnh góc vuông)
Suy ra $HB = HC$ (Hai cạnh tương ứng)
$\widehat{BAH} = \widehat{CAH}$ (hai góc tương ứng).
b) Xét hai tam giác vuông $ADH$ và $AEH$ có:
$AH$ là cạnh chung;
$\widehat{BAH} = \widehat{CAH}$ (cmt);
Suy ra $\Delta ADH=\Delta AEH$ (cạnh huyền - góc nhọn).
Suy ra $HD = HE$ (Hai cạnh tương ứng) nên $\Delta HDE$ cân tại $H$.

a, xét tam giác AHB và tam giác AHC có : ^AHC = ^AHB = 90
AB = AC do tam giác ABC cân tại A (gt)
AH chung
=> tam giác AHC = tam giác AHB (ch-cgv)
=> HB = HC (đn)
b, xét tam giác HEC và tam giác HDB có : ^HEC = ^HDB = 90
HC = HB (câu a)
^ABC = ^ACB do tam giác ABC cân tại A (gt)
=> tam giác HEC = tam giác HDB (ch-gn)
=> HE = HD (đn)
=> tam giác HED cân tại H (đn)
c, tam giác ABC cân tại A (gt) => = ^ACB = (180 - ^BAC) : 2 (tc)
^BAC= 120 (gt)
=> ^ACB = (180 - 120) : 2 = 30
tam giác vuông EHC vuông tại E (gt) => ^EhC = 90 - ^ACB
=> ^EHC = 60
^EHC = ^DHB
=> ^EHC = ^DHB = 60
^EHC + ^DHB + ^DHE = 180
=> ^DHE = 60
mà tam giác DHE cân tại H (câu b)
=> tam giác DHE đều
d, tam giác CEH = tam giác BDH (câu b)
=> CE = BD (đn)
AB = AC (câu a)
CE + EA = AC
BD + DA = AB
=> AE = AD
=> tam giác ADE cân tại A => ^AED = (180 - ^BAC) : 2
tam giác ABC cân tại A (gt) => ^ACB = (180 - ^BAC) : 2
=> ^AED = ^ACB mà 2 góc này đồng vị
=> DE//BC (đl)
hình em tự vẽ nhé
a) xét \(\Delta ABC\)cân tại A
=> \(AB=AC\)(t/c tam giác cân )
\(\Rightarrow\widehat{ABC}=\widehat{ACB}=\frac{180^o-\widehat{A}}{2}\)(t/c tam giác cân )
xét \(\Delta ABH\)và \(\Delta ACH\)
\(AB=AC\left(cmt\right)\)
\(\widehat{ABC}=\widehat{ACB}\left(cmt\right)\)
\(\widehat{AHB}=\widehat{AHC}\left(gt\right)\)
=>\(\Delta ABH\)=\(\Delta ACH\)(ch-gn)
=> HB=HC(2c tứ)
=> \(\widehat{BAH}=\widehat{CAH}\left(2gtu\right)\)
b) xét \(\Delta BHD\)và \(\Delta CHE\)
\(\widehat{BDH}=\widehat{CEH}\left(gt\right)\)
\(BH=HC\left(cmt\right)\)
\(\widehat{DBH}=\widehat{ECH}\left(cmt\right)\)
=>\(\Delta BHD\)=\(\Delta CHE\)(ch-gn)
=>HD=HE(2c tứ)
=> \(\Delta HDE\)cân tại H ( đ/n)
ta có \(\widehat{BAH}+\widehat{CAH}=\widehat{BAC}\)
lại có:\(\widehat{BAH}=\widehat{CAH}\left(2gtu\right)\)
mà \(\widehat{BAC}=120^o\)
=>\(\widehat{BAH}=\widehat{CAH}=60^o\)
xét \(\Delta ADH\)\(:\widehat{ADH}+\widehat{DAH}+\widehat{DHA}=180^o\)(đ/lý)
thay số :
rồi suy ra ^DHA = 30 độ(1)
xét nốt \(\Delta AHE\)rồi suy ra ^AHE=30 độ(2) ( cách làm tương tự tam giác ADH)
từ (1) và (2) =>\(\Delta\) DHE - \(\Delta\)đều
d) HD : chứng minh \(\Delta ADE\)cân tại A
=> \(\widehat{ADE}=\widehat{AED}=\frac{180^o-\widehat{A}}{2}\)
mà \(\Rightarrow\widehat{ABC}=\widehat{ACB}=\frac{180^o-\widehat{A}}{2}\)(cmt)
=> \(\widehat{ADE}=\widehat{ABC}\)
mà 2 góc này lại ở vị trí đồng vị của DE và BH
=> DE//BH
bye mik đi ngủ đây