Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

theo t/c góc ngoài tam giác ACB ta có:
ACM=CAB+ABC=180-2ABC+ABC=180-ABC
ABN=180-MAB(do BN//AM)
=180-ABC=> DPCM

a) Thấy 52=32+42 hay BC2=AB2+AC2
\(\Rightarrow\Delta ABC\) vuông tại A
b)Hình thì chắc bạn tự vẽ được nha![]()
![]()
![]()
Xét 2\(\Delta ABH\) và\(\Delta DBH\) có:
AB=DB
\(\widehat{BAH}=\widehat{BDH}\)
BH chung
\(\Rightarrow\Delta ABH=\Delta DBH\left(ch-cgv\right)\)
\(\Rightarrow\widehat{ABH}=\widehat{DBH}\)
\(\Rightarrow\)BH là tia phân giác \(\widehat{ABC}\)
c)tam giác ABC đã có các cạnh có độ dài khác nhau nên tam giác ABC ko cân được đâu chị
a) Ta có :
-BC2=52=25(1)
-AB2+AC2=32+42=25(2)
-Từ (1)và(2)suy ra BC2=AB2+AC2
-do đó tam giác ABC vuông tại A(áp dụng định lý Py-ta-go đảo)
-vậy tam giác ABC là tam giác vuông .
b)Xét \(\Delta\) ABH(vuông tại A) và \(\Delta\) DBH(vuông tại D) có
-BH là cạnh huyền chung
-AB=BD(gt)
-Do đó:\(\Delta\) ABH=\(\Delta\) DBH(cạnh huyền-cạnh góc vuông)
\(\Rightarrow\)Góc ABH =Góc DBH(hai góc tương ứng)
Vậy BH là tia phân giác của góc ABC

Tam giác ABC cân, mà C > 90 độ => Tam giác ABC cân tại C (nếu cân tại A hoặc B thì không tồn tại ABC, vì tổng 2 góc lớn hơn 180 độ là vô lí).
a. Vì ABC cân tại C, Cx p/giác góc C => Cx cũng là trung trực của ABC.
(Tự vẽ hình).
Xét 2 tam giác AMC & BMC có:
AC = BC (vì ABC cân tại C)
góc ACM = góc BCM (ABC cân tại C)
MC: cạnh chung
Do đó tam giác AMC = tam giác BMC (c.g.c)

Bài làm:
a) Xét tam giác ABH và tam giác ACH có:
Góc AHC = góc AHB = 90o
AB = AC
Vì AB = AC => tam giác ABC cân tại A => Góc B = góc C
Vậy tam giác ABH = tam giác ACH (c.huyền - góc nhọn)
=> HB = HC = 8 : 2 = 4 cm
Áp dụng định lí Py Ta go cho tam giác ABH vuông tại H ta có:
HA2 + HB2 = AB2
HA2 = AB2 - HB2
= 52 - 42 = 9
=> AH = \(\sqrt{9}=3cm\)
b) Xét tam giác DBH và tam giác ECH có:
BH = CH (chứng minh ở câu a)
Góc D = góc E = 90o
Góc B = góc C
Vậy tam giác DBH = tam giác ECH (c,huyền - g.nhọn)
=> HD = HE (2 cạnh tương ứng)
=> Tam giác HDE cân (tại H)
c) Vì tam giác DHB vuông tại D nên:
BH là cạnh lớn nhất (c.huyền)
=> BH > DH mà BH = CH
=> CH > DH
d) Vì GH = 1/3AH => G là trọng tâm của tam giác ABC
=> BN là đường trung tuyến
=> NA = NC
e) Ta có: GH = 1/3AH = 1/3 . 3 = 1 cm
Áp dụng định lí Py Ta Go cho tam giác GBH vuông tại H ta có:
HG2 + HB2 = BG2
BG2 = 12 + 42 = 17
=> BG = \(\sqrt{17}cm\)
Ta lại có: BG = 2/3 BN
=> BN = \(\frac{BG}{\frac{2}{3}}=\sqrt{17}.\frac{3}{2}=\frac{3\sqrt{17}}{2}cm\)

Đáp án A
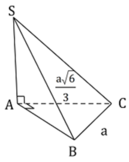
Em có: SA ⊥ ABC tại A
=> A là hình chiếu vuông góc của S trên (ABC)
=> AB là hình chiếu vuông góc của SB trên (ABC)


vẽ hình ra nha
ta có:\(\widehat{AFE}\) là góc ngoài tam giác AFB tại đỉnh F
\(\Rightarrow\widehat{AFE}=\widehat{FAB}+\widehat{ABF}\)
TA CÓ: GÓC FAB =20độ
góc ABF= 10 độ do BE là phân giác của góc ABC
\(\Rightarrow\widehat{AFE}=20^O+10^O=30^O\)
Ta có: \(\widehat{BAF}+\widehat{FAE}=\widehat{BAC}\)
TA cũng có: \(\widehat{BAF}=20^O\left(GIẢTHUYET\right)\)
\(\widehat{BAC}=50^O\)
=> \(\widehat{FAE}=50^O-20^0=30^O\)
xét tam giác FAE có 2 góc ở đáy cùng bằng 30 độ
=> tam giác FAE cân tại E

C/m 3 điểm thẳng hàng là tìm trọng tâm của tam giác đóa pạn, có trọng tâm ròi =>D,M.F thẳng hàng