Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

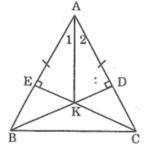
Xét ΔADB vuông tại D và ΔAEC vuông tại E, ta có:
AB = AC (giả thiết)
∠(BAC) chung
⇒ ΔADB = ΔAEC (cạnh huyền, góc nhọn)
⇒ AD = AE (hai cạnh tương ứng)
Xét ΔADK vuông tại D và ΔAEK vuông tại E có:
AD = AE (chứng minh trên)
AK cạnh chung
⇒ ΔADK = ΔAEK (cạnh huyền, cạnh góc vuông)
⇒ ∠(DAK) = ∠(EAK) (hai góc tương ứng)
Vậy AK là tia phân giác của góc BAC.

Bạn tự vẽ hình nhé!
Vì \(\Delta ABC\)cân tại A
\(\Rightarrow AB=AC\)
Xét 2 tam giác vuông \(AEC\)và \(ADB\)có:
\(AB=AC\left(cmt\right)\)
\(\widehat{A}\)là góc chung
\(\Rightarrow\Delta AEC=\Delta ADB\left(ch-gn\right)\)
\(\Rightarrow AE=AD\)( 2 cạnh tương ứng )
Xét 2 tam giác vuông \(AEK\)và \(ADK\)có:
\(AE=AD\left(cmt\right)\)
\(AK\)là cạnh chung
\(\Rightarrow\Delta AEK=\Delta ADK\left(ch-cgv\right)\)
\(\Rightarrow\widehat{EAK}=\widehat{DAK}\)( 2 góc tương ứng )
\(\Rightarrow AK\)là tia phân giác của góc A.

Bạn tự vẽ hình nhá.
Xét tam giác AEC vuông tại E và tam giác ADB vuông tại D ,có :
+ Góc A : góc chung
+ AC = AB ( tam giác ABC cân tại A)
Nên tam giác AEC = tam giác ADB (cạnh huyền - góc nhọn )
=> AE = AD (2 cạnh tương ứng)
Xét tam giác AEK vuông tại E và ADK vuông tại D, có :
+ AE = AD (cmt)
+ AK : cạnh chung
Nên tam giác AEK = ADK ( cạnh huyền - cạnh góc vuông)
=> góc EAK = góc KAD (2 góc tương ứng)
Vậy AK là tia phân giác của góc A.
bạn vào web này xem nha ( tham khảo ) http://olm.vn/hoi-dap/question/86792.html

Xét hai tam giác ADB và AEC có:
AB = AC (do \(\Delta ABC\) cân tại A)
\(\widehat{A}\): góc chung
Vậy: \(\Delta ADB=\Delta AEC\left(ch-gn\right)\)
Suy ra: AD = AE (hai cạnh tương ứng)
Xét hai tam giác vuông ADK và AEK có:
AK: cạnh huyền chung
AD = AE (cmt)
Vậy: \(\Delta ADK=\Delta AEK\left(ch-cgv\right)\)
Suy ra: \(\widehat{A_1}=\widehat{A_2}\) (hai góc tương ứng)
Do đó: AK là tia phân giác của góc A.
Giải
Xét tam giác EBC và tam giác DBC có:
E=D=90
B=C(gt)
BC là cạnh chung
=>tam giacs EBC=tam giác DBC( cạnh huyền-góc nhọn)
=>EC=DB( 2 cạnh TƯ)
Xét tam giác AEC và tam giác ADB có;
AB=AC(gt)
EC=BK(cmt)
AK cạnh chung
=> tam giác AEC=tam giác ADB(c.c.c)
=>B1=C1
Xét tam giác ABKvaf tam giác ACK có
AB=AC(gt)
AK chung
B1=C1(cmt)
=>tam giavs ABK=tam giác ACK(c.g.c)
=>A1=A2
=>AK là tia pg của góc A
(cmt: chứng minh trên)

Xét \(\Delta AEC\)và \(\Delta ADB\)có :
\(\widehat{E_1}=\widehat{D_1}=90^o(gt)\)
\(AC=AB(\Delta ABC\)cân \()\)
\(\widehat{BAC}\)chung
\(\Rightarrow\Delta AEC=\Delta ADB(ch-gn)\)
\(\Rightarrow AE=AD\)\((\)2 cạnh tương ứng \()\)
Xét \(\Delta AEK\)và \(\Delta ADK\)có :
\(\widehat{E_1}=\widehat{D_1}=90^o(gt)\)
\(AK\)chung
\(AE=AD(cmt)\)
\(\Rightarrow\Delta AEK=\Delta ADK(ch-cgv)\)
\(\Rightarrow\widehat{A_1}=\widehat{A_2}\)\((\)2 góc tương ứng \()\)
\(\Rightarrow\)AK là tia phân giác của \(\widehat{BAC}\)

a: Xét ΔADB vuông tại D và ΔAEC vuông tại E có
AB=AC
\(\widehat{BAD}\) chung
Do đó: ΔADB=ΔAEC
b: Xét ΔAEK vuông tại E và ΔADK vuông tại D có
AK chung
AE=AD
Do đó: ΔAEK=ΔADK
Suy ra: \(\widehat{EAK}=\widehat{DAK}\)
hay AK là tia phân giác của góc BAC
c: Ta có: EK+KC=EC
DK+KB=DB
mà EC=DB
và EK=DK
nên KB=KC
hay ΔKBC cân tại K

b,Xét 2 tam giác vuông AEC và ADB có :
AB = AC (gt)
^A : góc chung
=> tam giác AEC =tam giác ADB ( cạnh huyền - góc nhọn)
=> AE = AD ( 2 cạnh tương ứng )
Xét 2 tam giác vuông AEK và ADK có :
AK : cạnh chung
AE = AD ( cmt)
=> tam giác AEK = tam giác ADK ( cạnh huyền - cạnh góc vuông )
=> ^EAK = ^DAK ( 2 góc tương ứng )
=> AK là tia phân giác của góc A

a: Xét ΔBEC vuông tại E và ΔCDB vuông tại D có
BC chung
\(\widehat{EBC}=\widehat{DCB}\)
Do đó: ΔBEC=ΔCDB
b: Xét ΔABD vuông tại D và ΔACE vuông tại E có
AB=AC
BD=CE
Do đó: ΔABD=ΔACE
Xét ΔBEK vuông tại E và ΔCDK vuông tại D có
EB=DC
\(\widehat{EBK}=\widehat{DCK}\)
Do đó: ΔBEK=ΔCDK
c: Xét ΔBAK và ΔCAK có
BA=CA
AK chung
BK=CK
Do đó: ΔBAK=ΔCAK
Suy ra: \(\widehat{BAK}=\widehat{CAK}\)
hay AK là tia phân giác của góc BAC
Tự vẽ hình nha bạn
Ta có: tam giác ABC cân tại A
=> B = C
Ta có: Góc D = góc E = 90o (góc vuông)
K1 = K2 (2 góc đối đỉnh)
=> 180 - E - K1 = 180 - D - K2
=> B1 = C1
Vì B = C ; B1 = C1 => B - B1 = C - C1
=> B2 = C2
Vì B2 = C2 nên KBC cân tại K
=> KB = KC
Xét tam giác AKB và tam giác AKC có:
AK cạnh chung (1)
AB = AC (2)
BK = BC (3)
Từ (1) ; (2) ; (3) = > Tam giác AKB = tam giác AKC (c - c - c) (4)
Từ (4) = > A1 = A2 (2 góc tương ứng)
=> AK là tia phân giác của góc A
=> ĐPCM
Tớ sẽ bổ sung thêm hình sau
thế mà không biết à