Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có :
Tam giác ABC cân tại A
=> BAH=CAH
Ta lại có:
AI=AK
Gọi giao điểm của AH và IK là M
Xét ΔAIMΔAIM và ΔAKMΔAKM có:
AT=AK ( gt )
BAH=CAH(cmt)
AM chung
=> ΔAIMΔAIM= ΔAKMΔAKM (c.g.c)
=> IM=KM
=> I là đối xứng của K qua AH
(đ.p.c.m)
:))

Cho tam giác ABC cân tại A, đường cao AH. Trên cạnh AB lấy điểm D, trên cạnh AC lấy điểm E sao cho AD = AE. Chứng minh rằng: Δ ADC đối xứng với Δ AEB qua AH.

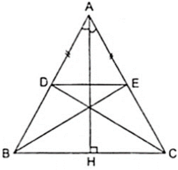
Vì Δ ABC cân tại A có AH là đường cao theo giả thiết nên AH cũng là đường phân giác của góc A.
Theo giả thiết ta có AD = AE nên Δ ADE cân tại A nên AH là đường trung trực của DE
⇒ D đối xứng với E qua AH.

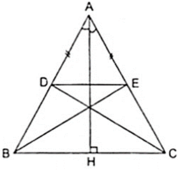
Vì Δ ABC cân tại A có AH là đường cao theo giả thiết nên AH cũng là trung trực của BC.
⇒ B đối xứng với C qua AH, E đối xứng với D qua AH.
Mặt khác, ta có A đối xứng với A qua AH theo quy ước.
⇒ Δ ADC đối xứng với Δ AEB qua AH.

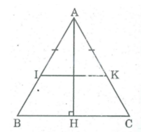
Ta có: △ ABC cân tại A; AH ⊥ BC (gt)
Suy ra: AH là tia phân giác của góc A
Lại có: AI = AK (gt)
Suy ra: ∆ AIK cân tại A
Do AH là tia phân giác của góc A
Nên AH là đường trung trực của IK
Vậy I đối xứng với K qua AH.

Gọi giao điểm của IK và AH là O.
Vì ΔABC cân tại A và AH là đường cao
=> AH đồng thời cũng là tia phân giác của ΔABC
hay AO là tia phân giác của \(\widehat{IAK}\)
=> \(\widehat{IAO}=\widehat{OAK}\)
Xét ΔAIO và ΔAKO có: \(\left\{{}\begin{matrix}AI=AK\left(gt\right)\\\widehat{IAO}=\widehat{KAO}\\AO
chung\end{matrix}\right.\)
=> ΔAIO = ΔAKO(c.g.c)
=>IO=KO(2 cạnh tương ứng)
Xét ΔAIK cân tại A (AI=AK) có AO là đường trung tuyến
=> AO là đương trung trực của \(\Delta\) AIK
=> I đối xứng với K qua AH
=>đpcm
Ta có: AI+IB=AB(I nằm giữa A và B)
AK+KC=AC(K nằm giữa A và C)
mà AI=AK(gt)
và AB=AC(ΔABC cân tại A)
nên IB=KC
Xét ΔABH vuông tại H và ΔACH vuông tại H có
AB=AC(ΔABC cân tại A)
AH chung
Do đó: ΔABH=ΔACH(Cạnh huyền-cạnh góc vuông)
Suy ra: BH=CH(Hai cạnh tương ứng)
Xét ΔIBH và ΔKCH có
IB=KC(cmt)
\(\widehat{B}=\widehat{C}\)(ΔBAC cân tại A)
BH=CH(cmt)
Do đó: ΔIBH=ΔKCH(c-g-c)
Suy ra: HI=HK(Hai cạnh tương ứng)
Ta có: AI=AK(gt)
nên A nằm trên đường trung trực của IK(Tính chất đường trung trực của một đoạn thẳng)(1)
Ta có: HI=HK(cmt)
nên H nằm trên đường trung trực của IK(Tính chất đường trung trực của một đoạn thẳng)(2)
Từ (1) và (2) suy ra AH là đường trung trực của IK
hay I đối xứng với K qua AH(đpcm)

Xét ΔABC cân tại A(gt).Mà AH là đường cao(gt)
=>AH cx là đường phân giác
=>^IAE=^KAE
Xét ΔIAE và ΔKAE có:
AI=AK(gt)
^IAE=^KAE(cmt)
AE:cạnh chung
=>ΔIAE=ΔKAE(c.g.c)
=>IE=KE (1)
Xét ΔAIK có AI=AK(gt)
=> ΔAIK cân tại A
Mà AE là đường pg
=>AE cx là đường cao
=> IK\(\perp\)AH (2)
Từ (1) và (2) suy ra:
I đối xứng với K qua AH

Ta có :
Tam giác ABC cân tại A
=> BAH=CAH
Ta lại có:
AI=AK
Gọi giao điểm của AH và IK là M
Xét ΔAIMΔAIM và ΔAKMΔAKM có:
AT=AK ( gt )
BAH=CAH(cmt)
AM chung
=> ΔAIMΔAIM= ΔAKMΔAKM (c.g.c)
=> IM=KM
=> I là đối xứng của K qua AH
(đ.p.c.m)
:))
Ta có :
Tam giác ABC cân tại A
=> BAH=CAH
Ta lại có:
AI=AK
Gọi giao điểm của AH và IK là M
Xét ΔAIMΔAIM và ΔAKMΔAKM có:
AT=AK ( gt )
BAH=CAH(cmt)
AM chung
=> ΔAIMΔAIM= ΔAKMΔAKM (c.g.c)
=> IM=KM
=> I là đối xứng của K qua AH
(đ.p.c.m)