Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Xét ΔABH vuông tại H và ΔACH vuông tại H có
AB=AC(ΔBAC cân tại A)
AH chung
Do đó: ΔABH=ΔACH(Cạnh huyền-cạnh góc vuông)
b) Xét ΔAMD và ΔCMH có
MA=MC(gt)
\(\widehat{AMD}=\widehat{CMH}\)(hai góc đối đỉnh)
MD=MH(gt)
Do đó: ΔAMD=ΔCMH(c-g-c)
Suy ra: AD=HC(Hai cạnh tương ứng)
c) Ta có: ΔAMD=ΔCMH(cmt)
nên \(\widehat{MAD}=\widehat{MCH}\)(hai góc tương ứng)
mà hai góc này là hai góc ở vị trí so le trong
nên AD//HC(Dấu hiệu nhận biết hai đường thẳng song song)
hay AD//HB
Xét tứ giác ABHD có
AD//BH(cmt)
AD=BH(=HC)
Do đó: ABHD là hình bình hành(Dấu hiệu nhận biết hình bình hành)
Suy ra: AB//DH(Hai cạnh đối)

Ta có:
- AB = AC (tam giác ABC vuông tại A)
- AM là trung tuyến của tam giác ABC (điểm M là trung điểm của BC)
- MN vuông góc AC và MN = MH
Khi đó, ta có:
- Tam giác ABM và ACM là hai tam giác cân (AB = AM và AC = AM), nên AM là đường trung trực của đoạn BM và đoạn CM.
- Gọi I là giao điểm của đường thẳng MN và BC. Ta có MI là đường trung trực của đoạn BC.
- Vì MN = MH nên tam giác MHN là tam giác cân tại M, nên đường trung trực của đoạn HN cũng là đường trung trực của đoạn BC, do đó đường trung trực của đoạn HN cũng cắt đường trung trực của đoạn BC tại I.
Do AM là đường trung trực của đoạn BM và đoạn CM, và MI là đường trung trực của đoạn BC, nên ta có AM và MI là hai đường trùng nhau, do đó A, M, I thẳng hàng.
Từ đó suy ra:
- Góc AMB = góc AMC (do AM là đường trung trực của đoạn BM và đoạn CM)
- Góc AHB = góc AHC (do AB = AC và HN là đối của MN)
- Góc AMB + góc AHB = 90 độ (do MN vuông góc AC)
- Góc AMC + góc AHC = 90 độ (do MN vuông góc AC)
Vậy ta có:
góc AMB + góc AHB = góc AMC + góc AHC
Do đó, tam giác AMB bằng tam giác AMC theo trường hợp góc - góc - góc của hai tam giác.
- Vì AM là trung tuyến tam giác ABC (gt)
=> BM = CM (định nghĩa)
- Xét tam giác AMB và tam giác AMC, có:
+ BM = CM (cmt)
+ AB = AC (gt)
+ Chung AM
=> tam giác AMB = tam giác AMC (ccc)
- Vậy tam giác AMB = tam giác AMC theo trường hợp cạnh - cạnh - cạnh

a: XétΔABM và ΔACM có
AB=AC
BM=CM
AM chung
Do đó:ΔABM=ΔACM
b: Ta có: ΔABC cân tại A
mà AM là đường trung tuyến
nên AM là đường trung trực của BC
c: Xét ΔMCE có
CH là đường cao
CH là đường trung tuyến
Do đó: ΔMCE cân tại C
mà CA là đường cao
nên CA là tia phân giác của góc MCE

a: Xét ΔABC vuông tại A và ΔADE vuông tại A có
AB=AD
AC=AE
Do đó: ΔABC=ΔADE
b: Xét ΔAMD và ΔANB có
AM=AN
MD=NB
AD=AB
Do đó: ΔAMD=ΔANB

Ai đó giúp mình với! Mình đang cần gấp!:( Các bạn vẽ hình lun giúp mình nha! Cảm ơn các bạn nhìu!:)
Do tam giác ABC có
AB = 3 , AC = 4 , BC = 5
Suy ra ta được
(3*3)+(4*4)=5*5 ( định lý pi ta go)
9 + 16 = 25
Theo định lý py ta go thì tam giác abc vuông tại A
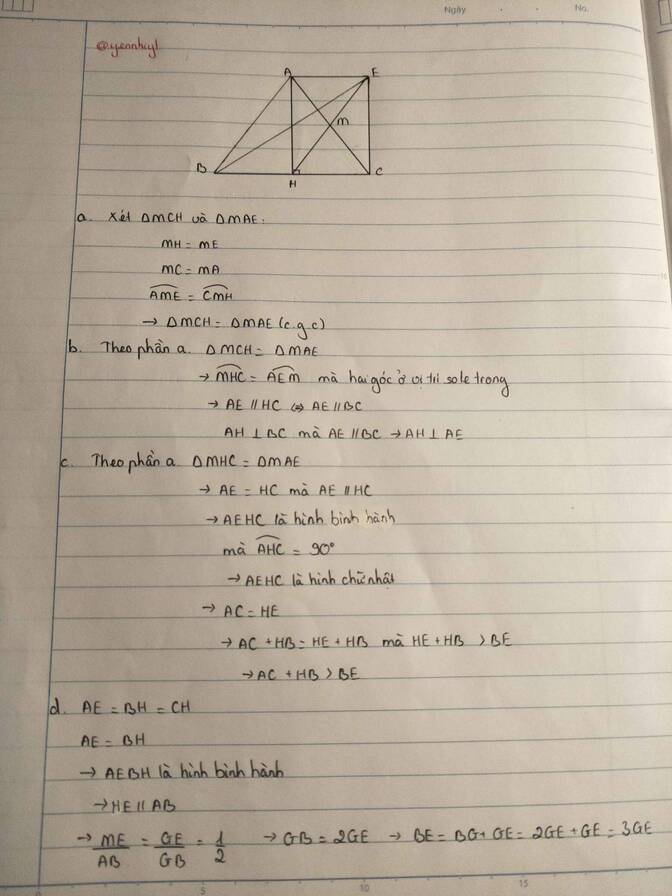
a: Xét ΔMCH và ΔMAE có
MC=MA
\(\widehat{CMH}=\widehat{AME}\)
MH=ME
Do đó: ΔMCH=ΔMAE
b: Ta có: ΔMCH=ΔMAE
nên \(\widehat{MCH}=\widehat{MAE}\)
mà hai góc này là hai góc ở vị trí so le trong
nên HC//AE
hay BC//AE
Ta có: ΔBAC cân tại A
mà AM là đường trung tuyến ứng với cạnh đáy BC
nên AH\(\perp\)BC
mà BC//AE
nên AH\(\perp\)AE