Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Tham khảo
6 tháng 2 2017 lúc 14:19
Cho tam giác ABC cân tại A , góc A=20 độ , vẽ tam giác đều DBC , D nằm trong tam giác ABC . Tia phân giác của góc ABD cắt AC tại H . Chứng minh :
a) Tia AD là tia phân giác của góc BAC
b) AM = BC
Hình thì chắc bạn vẽ được nên tớ không vẽ nữa!!!![]()
![]()
![]()
a, Đi chứng minh tam giác ABD=tam giác ACD (c.c.c) =>góc BAD=góc CAD=>AD là tia phân giác của góc BAC(đpcm)
nếu có j thắc mắc hỏi mình nha!!!![]()
![]()
b, tớ sửa đề chứng minh AH=BC do không có điểm M.
Chứng minh
Xét tam giác ABC cân tại A ta có:
góc ABC=góc ACB=(180độ -20 độ):2=160 độ:2=80độ (theo tính chất của tam giác cân)
ta lại có: góc DBC=60 độ( theo tính chất của tam giác đều)
mà góc ABD=góc ABC-góc DBC=80độ -60 độ=20độ
mặt khác góc BAD=gócCAD=20độ/2=10độ và góc ABD=20độ/2=10độ (theo tính chất của tia phân giác)
Xét tam giác ABH và tam giác BAD ta có:
góc BAH=góc ABD (=20độ); AB: cạnh chung; góc ABH=góc BAD(=10độ)
Do đó tam giác ABH = tam giác BAD
=> AH=BD mà BD=BC( theo tính chất của tam giác đều) nên AH=BC (đpcm)
Có chỗ nào vướng mắc hỏi mình nha!! Chúc bạn học giỏi!!![]()
![]()

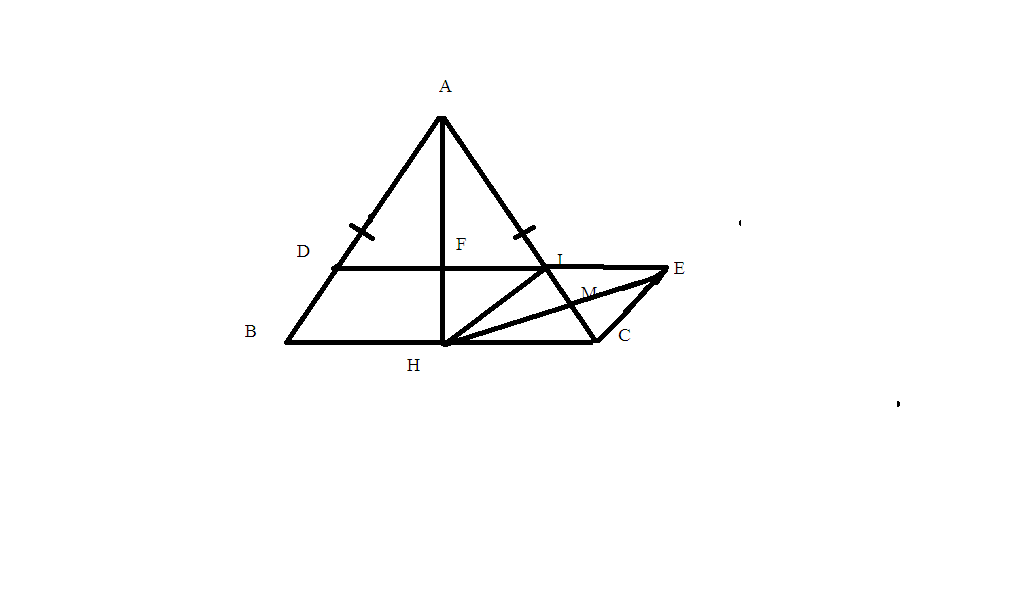
a) Xét ΔABH và ΔACH có:
AB=AC (ΔABC cân tại A)
AH là cạnh chung
HB=HC(H là trung điểm của BC)
Nên ΔABH =ΔACH (c.c.c)
=>\(\widehat{AHB}=\widehat{AHC}\)( 2 GÓC TƯƠNG ỨNG)
Ta có: \(\widehat{AHB}+\widehat{AHC}=180^O\)( 2 góc kề bù)
=>\(\widehat{AHB}.2=180^O\Rightarrow\widehat{AHB}=90^O\)
=>AH ⊥ BC
b) Vì ΔABH =ΔACH => \(\widehat{BAH}=\widehat{CAH}\)
Ta có: AD+BD=AB ( D nằm giữa A và B)
AI+IC=AC( I nằm giữa A và C)
Mà AB=AC, BD=IC =>AD=AI
Cho AH và DI cắt nhau tại F
Xét ΔDFA và ΔIFA có:
FA là cạnh chung
\(\widehat{BAH}=\widehat{CAH}\)
AD=AI
Nên ΔDFA=ΔIFA (c.g.c)
=>\(\widehat{DAF}=\widehat{IAF}\)
=>A là tia phân giác của góc DHI

a) Xét ΔABDΔABD và ΔACEΔACE có:
AB=ACAB=AC (do ΔABCΔABC cân đỉnh A)
ˆABD=ˆACEABD^=ACE^ (cùng +45o+45o=180^o)
BD=CEBD=CE (giả thiết)
⇒ΔABD=ΔACE⇒ΔABD=ΔACE (c.g.c)
⇒AD=AE⇒AD=AE (hai cạnh tương ứng)
⇒ΔADE⇒ΔADE cân đỉnh A
b) Ta có: BD+BM=CE+CM⇒DM=EMBD+BM=CE+CM⇒DM=EM
Xét ΔAMDΔAMD và ΔAMEΔAME có:
AD=AEAD=AE (cmt)
AMAM chung
DM=EMDM=EM (cmt)
⇒ΔAMD=ΔAME⇒ΔAMD=ΔAME (c.c.c)
⇒ˆMAD=ˆMAE⇒MAD^=MAE^ (hai góc tương ứng)
⇒AM⇒AM là phân giác ˆDAEDAE^ (đpcm)
Ta có ΔAMD=ΔAME⇒ˆAMD=ˆAMEΔAMD=ΔAME⇒AMD^=AME^
Mà ˆAMD+ˆAME=180oAMD^+AME^=180o
⇒ˆAMD=ˆAME=180o2=90o⇒AMD^=AME^=180o2=90o
⇒AM⊥DE⇒AM⊥DE (đpcm)
c) Xét ΔΔ vuông ABHABH và ΔΔ vuông ACKACK có:
AB=ACAB=AC (gt)
ˆBAH=ˆCAKBAH^=CAK^ (do ΔABD=ΔACEΔABD=ΔACE)
⇒ΔABH=ΔACK⇒ΔABH=ΔACK (ch-gn)
⇒BH=CK⇒BH=CK (hai cạnh tương ứng) (đpcm)
CHÚC BẠN HỌC GIỎI NHÉ THEO DÕI CHÉO NHA?
a) Trên BC lấy điểm A' và A'' sao cho BA' = BA; BA'' = BD
Do BD là phân giác góc ABA' nên ta có ngay \(\Delta ABD=\Delta A'BD\left(c-g-c\right)\)
\(\Rightarrow AD=A'D\) ; \(\widehat{BA'D}=\widehat{BAD}=180^o-40^o.2=100^o\)
\(\Rightarrow\widehat{DA'A''}=80^o\)
Xét tam giác cân BDA'' có: \(\widehat{DBA''}=20^o\Rightarrow\widehat{BA''D}=\frac{180^o-20^o}{2}=80^o\)
Suy ra DA' = DA'' và \(\widehat{A''DC}=\widehat{DA''A'}-\widehat{ACB}=40^o\)
Nên DA'' = CA''
Tóm lại thì AD = DA' = DA'' = A''C nên BC = BA''+ A''C = BD + AD
b) Vẽ tam giác đều AMF.
Ta có ngay \(\widehat{MAF}=60^o\Rightarrow\widehat{CAF}=100^o-60^o=40^o\)
Suy ra \(\Delta ABC=\Delta CAF\left(c-g-c\right)\)
\(\Rightarrow AC=CF\)
Từ đó ta có \(\Delta AMC=\Delta FMC\left(c-c-c\right)\)
\(\Rightarrow\widehat{AMC}=\widehat{FMC}\) hay MA là phân giác óc AMF.
Vậy nên \(\widehat{MAC}=30^o\)
Làm ơn giúp mk với ạ cảm ơn các bạn nhiều