Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

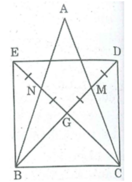
* Tam giác ABC có hai đường trung tuyến BM và CN cắt nhau tại G
Suy ra: G là trọng tâm của ∆ ABC .
⇒ GB = 2GM (tính chất đường trung tuyến)
GC = 2GN (tính chất đường trung tuyến)
Điểm D đối xứng với điểm G qua điểm M
⇒ MG = MD hay GD = 2GM
Suy ra: GB = GD (l)
Điểm E đối xứng với điểm G qua điểm N
⇒ NG = NE hay GE = 2GN
Suy ra: GC = GE (2)
Từ (1) và (2) suy ra tứ giác BCDE là hình bình hành (vì có hai đường chéo cắt nhau tại trung điểm mỗi đường)
Xét ∆ BCM và ∆ CBN, có: BC cạnh chung
∠ (BCM) = ∠ (CBN) (tính chất tam giác cân)
CM = BN (vì AB = AC)
Suy ra: ∆ BCM = ∆ CBN (c.g.c)
⇒ ∠ (MBC) = ∠ (NCB) ⇒ ∆ GBC cân tại G ⇒ GB = GC ⇒ BD = CE
Hình bình hành BCDE có hai đường chéo bằng nhau nên nó là hình chữ nhật.

Tự vẽ hình:
cminh:Vì D đối xứng với G qua M
=>GM=MD Hay GD=2GM
Vì BM;CN cắt nhau tại G trong tam giác ABC
=>G là trọng tâm trong Tam giác ABC =>BG=2GM
Suy ra : GD=BG(vì =2GM)=> G là trung điểm của BD (1)
Ta lại có : E đối xứng với G qua N=> EN=GN Hay EG=2NG
Và CG=2GN( G là trọng tâm)
Suy ra: CG=EG ( vì =2NG) (2) (*)
Từ (1) (2)=> Tứ giác BEDC là hình bình hành
Xét \(\Delta\)CBM Và \(\Delta\)BCN Có:
BC: Cạnh chung
Góc B=C(g/t)
BN=CM(AB=AC)
=> hai tam giác bằng nhau(c-g-c)
=>MBC=NCB(2 góc tương ứng) hay tam giác GBC cân=> BG=GC (**)
Từ (*) (**)=> Hình bình hành BEDC là hình chữ nhật

a)
Xét tứ giác MNPQ có
G là trung điểm của đường chéo MP(gt)
G là trung điểm của đường chéo NQ(gt)
Do đó: MNPQ là hình bình hành(Dấu hiệu nhận biết hình bình hành)
b)
Xét ΔABC có
BM là đường trung tuyến ứng với cạnh AC(gt)
CN là đường trung tuyến ứng với cạnh AB(gt)
BM cắt CN tại G(gt)
Do đó: G là trọng tâm của ΔABC(Định lí ba đường trung tuyến của tam giác)
Suy ra: \(MG=\dfrac{1}{3}MB;BG=\dfrac{2}{3}MB;NG=\dfrac{1}{3}NC;CG=\dfrac{2}{3}NC\)(1)
Ta có: G là trung điểm của MP(gt)
nên MG=GP
mà \(MG=\dfrac{1}{3}MB\)
nên \(MG=GP=\dfrac{1}{3}MB\)
Ta có: MG+GP=MP(G nằm giữa M và P)
nên \(MP=\dfrac{1}{3}MB+\dfrac{1}{3}MB=\dfrac{2}{3}MB\)(1)
Ta có: G là trung điểm của NQ(gt)
nên \(GN=GQ=\dfrac{1}{3}NC\)
Ta có: NG+GQ=NQ(G là trung điểm của NQ)
nên \(NQ=\dfrac{1}{3}NC+\dfrac{1}{3}NC=\dfrac{2}{3}NC\)(2)
Ta có: \(AN=NB=\dfrac{AB}{2}\)(N là trung điểm của AB)
\(AM=MC=\dfrac{AC}{2}\)(M là trung điểm của AC)
mà AB=AC(ΔBAC cân tại A)
nên AN=NB=AM=MC
Xét ΔAMB và ΔANC có
AB=AC(ΔABC cân tại A)
\(\widehat{BAM}\) chung
AM=AN(cmt)
Do đó: ΔAMB=ΔANC(c-g-c)
Suy ra: BM=CN(hai cạnh tương ứng)(3)
Từ (1), (2) và (3) suy ra NQ=MP
Hình bình hành MNPQ có NQ=MP(cmt)
nên MNPQ là hình chữ nhật(Dấu hiệu nhận biết hình chữ nhật)

a) Vì BM là đường trung tuyến AC (gt)=>AM=CM
Vì CN là đường trung tuyến AB(gt)=>AN=BN
=>MN là đường trung bình tam giác ABC
=>MN//BC, MN=1/2 BC (điều1)
Ta lại có:
G là trung điểm MP(vì P là điểm đối xứng vs M qua G
=>PG=GM
VÌ GM=1/2 BG
PG=GM
=>BP=PG
Làm tương tự:GQ=CQ
Ta có:BP=PG(cmt)
GQ=CQ (cmt)
=>PQ là đường trung bình tam giác BGC
=>PQ//BC, PQ=1/2 BC (điều 2)
Từ 1 và 2 điều trên =>MN=PQ(cug=1/2 BC)
MN//PQ(cug //BC)
=>MNPQ lầ hình bình hành (t/c hbh )
b)Nếu tam giác ABC cân tại A thì AG vuông góc BC
=>PN vuông góc vs BC.Mặt khác PQ//BC
=>PN vuông góc vs PQ mà MNPQ là hình bình hành(cmt)
lại có 1 góc =90độ=>MNPQ là hình chữ nhật

Xét tứ giác BCDE có
G là trung điểm của BD
G là trung điểm của CE
Do đó: BCDE là hình bình hành
mà \(\widehat{EBC}=90^0\)
nên BCDE là hình chữ nhật
MK dang thac mac tai sao mk lai co the lam ging het bn 100% ?