Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
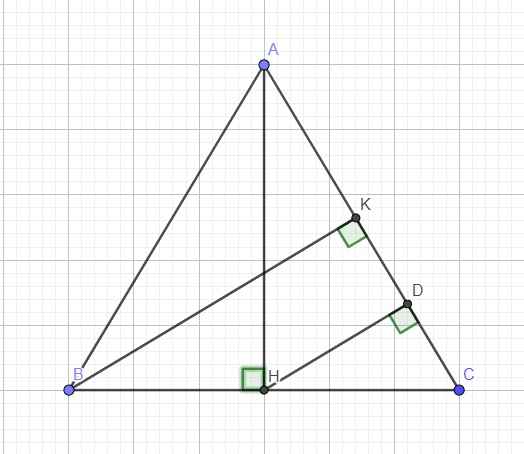
cho tam giac ABC cân tại A , AH vuông góc với BC , BK vuông góc với AC , AH=15,6 ; BK=12 . Tính BC ?


a: AH*BC=BK*AC
=>BC/AC=BK/AH=6/5
=>BH/AC=3/5
=>CH/AC=3/5
=>CH/3=AC/5=k
=>CH=3k; AC=5k
AH^2+HC^2=AC^2
=>16k^2=32^2=1024
=>k^2=64
=>k=8
=>CH=24cm; AC=40cm
=>BC=48cm; AB=40cm
b: Xét ΔCKB vuông tại K và ΔCHA vuông tại H có
góc C chung
=>ΔCKB đồng dạng với ΔCHA
=>CK/CH=CB/CA
=>CK*CA=CH*CB=1/2BC^2
=>2*CK*CA=BC^2


Từ H kẻ \(HD\perp AC\Rightarrow HD||BK\) (cùng vuông góc AC)
Mà ABC cân tại A \(\Rightarrow\) H là trung điểm BC \(\Rightarrow HC=\dfrac{BC}{2}\)
\(\Rightarrow\) HD là đường trung bình tam giác BCK
\(\Rightarrow HD=\dfrac{BK}{2}\)
Áp dụng hệ thức lượng trong tam giác vuông ACH với đường cao HD ứng với cạnh huyền:
\(\dfrac{1}{HD^2}=\dfrac{1}{AH^2}+\dfrac{1}{CH^2}\)
\(\Leftrightarrow\dfrac{1}{\left(\dfrac{BK}{2}\right)^2}=\dfrac{1}{AH^2}+\dfrac{1}{\left(\dfrac{BC}{2}\right)^2}\)
\(\Leftrightarrow\dfrac{4}{BK^2}=\dfrac{1}{AH^2}+\dfrac{4}{BC^2}\)
\(\Leftrightarrow\dfrac{1}{BK^2}=\dfrac{1}{BC^2}+\dfrac{1}{4AH^2}\)

+AH.BC = AC.BK => BC =6/5 AC (1)
+ Pi ta go HAC => \(\left(\frac{BC}{2}\right)^2=AC^2-AH^2\Leftrightarrow4AC^2-BC^2=4.10^2\) (2)
(1)(2) => AC =25/2 ; BC =15
=> CABC = BC + AC+AB =BC+2AC = 15 +25 =40

kẻ 1 đường thẳng vuông góc với BC cắt AC ở E
Xét tam giác CBE vuông tại B có:
1/BK^2=1/BC^2+1/BE^2 (hệ thức lượng)(1)
ta lại có:
*AH vuông góc với BC
BE vuông góc với BC
=>AH//BE (2)
*tam giác ABC cân tại A có:
AH là đường cao của tam gic1 ABC nên:
AH cũng là đường trung tuyến của tam giác ABC
=>H là trung điểm của BC (3)
từ (2) và (3) suy ra:
A là trung điểm của CE (4)
từ (3) và (4) suy ra:
AH là đường trung bình của tam giác CBE
=> AH=BE/2
=>BE=2AH
=>BE2=4AH2 (5)
từ (1) và (5) suy ra:
1/BK^2=1/BC^2+1/4AH^2

Áp dụng công thức tính diện tích tam giác ta có:
\(S_{ABC}\) =\(\frac{1}{2}\).AH.BC= \(\frac{1}{2}\).BK.AC
<=> \(\frac{1}{2}\).6.BC= \(\frac{1}{2}\).5.AC
<=> AC= \(\frac{6.BC}{5}\)(1)
Mà trong tam giác ABC cân tại A thì đường cao AH cũng là đường trung tuyến => HC=\(\frac{BC}{2}\)(2)
ÁP dụng định lý pytago vào trong tam giác vuông AHC ta có:
\(AC^2\)=\(AH^2\)+\(HC^2\)
từ (1) và (2) ta có:
<=>\(\left(\frac{6BC}{5}\right)^2\)=\(6^2\)+\(\left(\frac{BC}{2}\right)^2\)
<=>\(\frac{36BC^2}{25}\)-\(\frac{BC^2}{4}\)=36
<=>\(\frac{119BC^2}{100}\)=36
<=> \(BC^2\)=\(\frac{3600}{119}\)
<=> BC=\(\sqrt{\frac{3600}{119}}\)=\(\frac{60}{\sqrt{119}}\)