Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Xét ΔABH vuông tại H và ΔACH vuông tại H có AB=AC(ΔABC cân tại A)
AH chung
Do đó: ΔABH=ΔACH(cạnh huyền-cạnh góc vuông)

XÉT TAM GIÁC AHB VÀ TAM GIÁC AHC CÓ
AB=AC(GT)
AH CHUNG
GÓC AHB = GÓC AHC
=>TAM GIÁC AHB=TAM GIÁC AHC (CGC)
C,XÉT TAM GIÁC AHE VÀ TAM GIÁC AFH CÓ
AH CHUNG
GÓC AEH=GÓC AFH =90*
A1=A2
=>TAM GIÁC AHE=TAM GIÁC AFH (GCG)
=>HE=HF (CẠNH TƯƠNG ỨNG)

a: Xét ΔAHB vuông tại H và ΔAHC vuông tại H có
AB=AC
AH chung
Do đó: ΔAHB=ΔAHC
b: Xét ΔAKH vuông tại K và ΔAFH vuông tại F có
AH chung
\(\widehat{KAH}=\widehat{FAH}\)
Do đó: ΔAKH=ΔAFH
Suy ra: HK=HF
c: Xét ΔABC có AK/AB=AF/AC
nên KF//BC

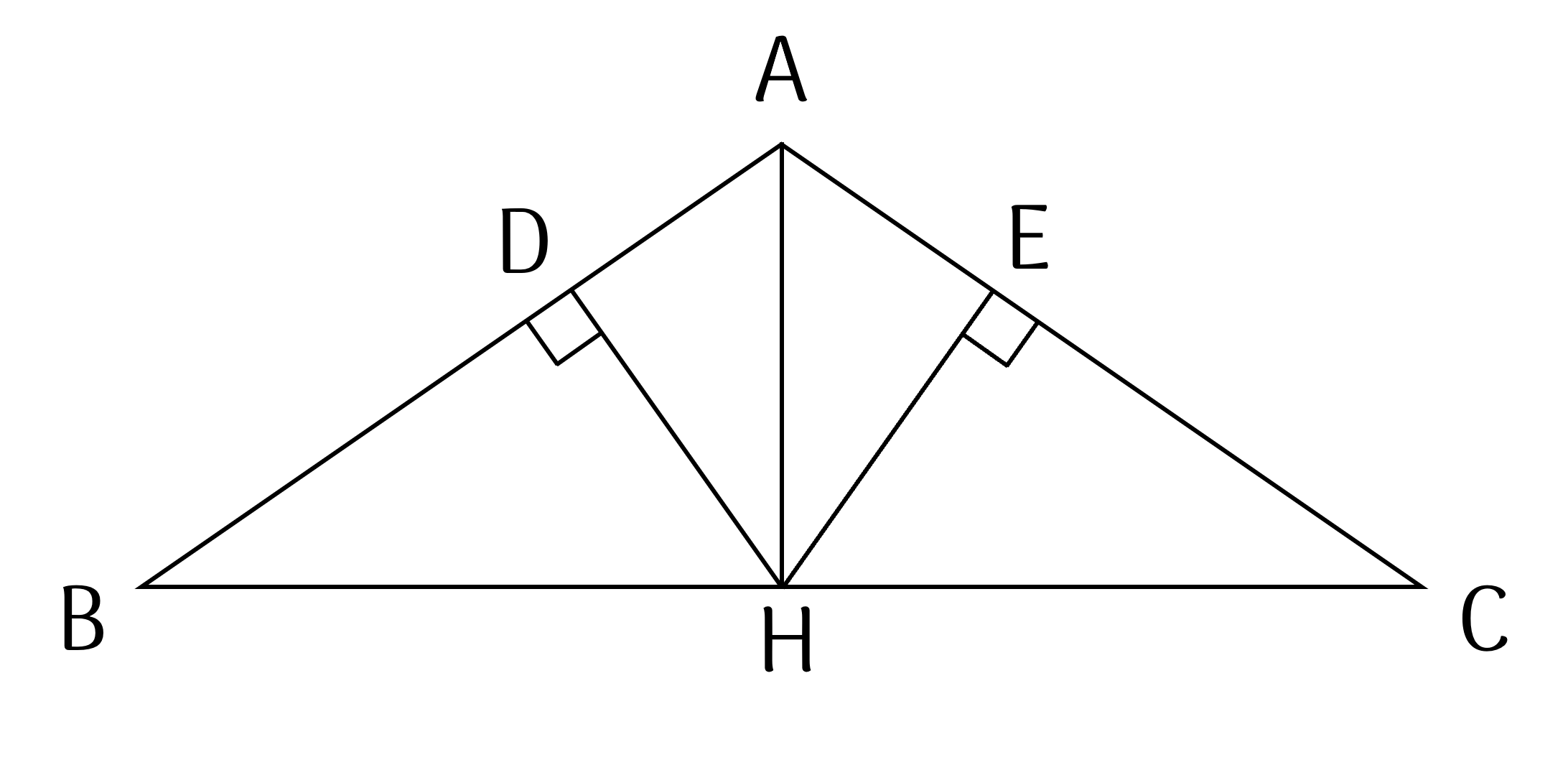
a) Xét hai tam giác vuông $AHB$ và $AHC$ có:
$AH$ là cạnh chung;
$AB = AC$ (gt);
Suy ra $\Delta AHB=\Delta AHC$ (cạnh huyền - cạnh góc vuông)
Suy ra $HB = HC$ (Hai cạnh tương ứng)
$\widehat{BAH} = \widehat{CAH}$ (hai góc tương ứng).
b) Xét hai tam giác vuông $ADH$ và $AEH$ có:
$AH$ là cạnh chung;
$\widehat{BAH} = \widehat{CAH}$ (cmt);
Suy ra $\Delta ADH=\Delta AEH$ (cạnh huyền - góc nhọn).
Suy ra $HD = HE$ (Hai cạnh tương ứng) nên $\Delta HDE$ cân tại $H$.

a: Xét ΔAHB vuông tại H và ΔAHC vuông tại H có
AB=AC
AH chung
Do đó: ΔAHB=ΔAHC
b: Ta có: ΔABH=ΔACH
nên HB=HC và \(\widehat{BAH}=\widehat{CAH}\)
c: Xét ΔHKB vuông tại K và ΔHIC vuông tại I có
HB=HC
\(\widehat{B}=\widehat{C}\)
Do đó: ΔHKB=ΔHIC

a) Vì AB = AC =10cm => (đpcm)
b) Xét \(\Delta AHB\)và \(\Delta AHC\)có;
AB = AC(gt)
\(\widehat{AHB}=\widehat{AHC}=90^o\)
AH chung
\(\Rightarrow\Delta AHB=\Delta AHC\left(c.g.c\right)\)
\(\Rightarrow HB=HC\)(2 cạnh tương ứng)(1)
\(\Rightarrow\widehat{B}=\widehat{C}\)(2 góc tương ứng)(2)
\(\Rightarrow\widehat{BAH}=\widehat{CAH}\Rightarrow\)AH là tia phân giác của \(\widehat{A}\)
c) HM với HN?
Vì \(\Delta HMB;\Delta HNC\)là tam giác vuông nên từ (1);(2) =>\(\Delta HMB=\Delta HNC\)
e)Xét \(\Delta AHC\)vuông:
Áp dụng định lí Py ta go ta có:
\(AC^2=CH^2+AH^2\)
\(12^2=6^2+AH^2\)
\(\Rightarrow AH^2=12^2-6^2=144-36=108\)
\(\Rightarrow AH=\sqrt{108}cm\)

Xét tgAHB và tg AHC có:
+AB=AC(gt)
+AH là cạnh chung
+góc BHA=góc CHA
=>tgAHB=tg AHC(c-g-c)
=>HB=HC,góc BAH=góc CAH
Các cặp tg vuông là:
BEH-HFC,VÌ HE và HC là 2 đường cao=>tgBEH và tgCFH là cặp tg vuông(g-c-g)
Gọi k là giao điểm của HA và EF,=>tgEHF là tg cân=>góc HEF=góc EFH=>EK=EF
=>MÀ AB=AC,EB=FC=>AE=AF=>Tg AEF là tg cân=>AK cũng là đường CAO
=> tgAEK và tg AFK là cặp tg vuông(c-g-c)
=>tg EKH Và tg EFH là cặp tg vuông(g-c-g)
=>tg AEH và tg AFH là cặp tg vuông(c-g-c)
Và cuối cùng là tg ABH và tg ACH(c-g-c)
+vì EF vuông góc với KH(cmt)và BC cũng vuông góc với KH=>EF//BC(ĐPCM)
a, Xét tam giác AHB và tam giác AHC có:
AH chung
AB=AC (tam giác ABC cân tại A)
Vậy tam giác AHB= tam giác AHC (cạnh huyền-góc nhọn)
b,từ CMT: ta có:
HB=HC
Góc BAH= góc CAH
c,tam giác AHF=tam giác AHE(cạnh huyền AH chung,góc nhọn BAH =góc nhọn CAH)
tam giác AHC= tam giác AHB(cạnh huyền AH chung, góc nhọn BAH =góc nhọn CAH)
tam giác BEH =tam giác HFC(cạnh huyền BH=CH, góc nhọn EBH = góc nhọn FCH)
d,sorry bạn, câu này mik ko làm đc