Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
a, Xét tam giác BAC và tam giác BEA ta có
^B _ chung
^BAC = ^BEA = 900
Vậy tam giác BAC ~ tam giác BEA (g.g)
b, Theo định lí Pytago tam giác ABC vuông tại A
\(BC=\sqrt{AB^2+AC^2}=25cm\)
Ta có \(S_{ABC}=\dfrac{1}{2}.AB.AC;S_{ABC}=\dfrac{1}{2}.AH.BC\Rightarrow AH=\dfrac{AB.AC}{BC}=\dfrac{300}{25}=12cm\)
Vì BE ⊥ BD nên BE là đường phân giác góc ngoài tại đỉnh B
Suy ra :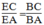 
( t/chất đường phân giác)
Suy ra: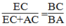 
⇒ EC.BA= BC (EC + AC)
Suy ra: EC.BA - EC.BC = BC.AC ⇒EC (BA - BC) = BC.AC
Vậy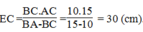 
Xét \(\Delta ABC\) vuông tại A có \(AB^2+AC^2=BC^2\) (định lý Pytago)
\(\Rightarrow BC^2=12^2+16^2=20^2\Rightarrow BC=20\).
Theo tính chất đường phân giác trong tam giác ABC ta có:
\(\dfrac{BD}{AB}=\dfrac{CD}{AC}=\dfrac{CD+BD}{AC+AB}=\dfrac{BC}{AC+AB}=\dfrac{20}{12+16}=\dfrac{5}{7}\Rightarrow BD=\dfrac{60}{7};CD=\dfrac{80}{7}\).
Ta có \(AH.BC=AB.AC\left(=2S_{ABC}\right)\Rightarrow AH=\dfrac{AB.AC}{BC}=\dfrac{48}{5}\).
Từ đó \(BH=\sqrt{AB^2-AH^2}=\sqrt{12^2-\left(\dfrac{48}{5}\right)^2}=\dfrac{36}{5}\).
Suy ra \(HD=\left|BD-BH\right|=\left|\dfrac{48}{5}-\dfrac{36}{5}\right|=\dfrac{12}{5}\).
\(AD=\sqrt{AH^2+HD^2}=\dfrac{12\sqrt{17}}{5}\).
\(AC=\sqrt{12^2+16^2}=20\left(cm\right)\)
AK là phân giác
=>BK/AB=CK/AC
=>BK/3=CK/5=16/8=2
=>BK=6cm
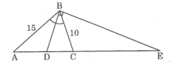
Vì AD là đường phân giác của tam giác BAC nên ta có:
\(\dfrac{AB}{AC}=\dfrac{BD}{DC}hay\dfrac{12}{15}=\dfrac{7}{DC}\Rightarrow DC=\dfrac{12}{15}.7=5,6cm\)
Suy ra BC=BD+DC hay BC=7+5,6 \(\Rightarrow BC=12,6cm\)
Vậy BC = 12,6 cm
hình bạn tự vẽ nhá!