Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

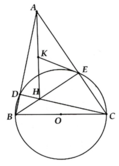
1) Vì AB là đường kính \(\Rightarrow\angle AMB=90\)
\(\Rightarrow\angle EHB+\angle EMB=90+90=180\Rightarrow EMBH\); nội tiếp
b) Vì AB là đường kính \(\Rightarrow\angle ACB=90\)
\(\Rightarrow\Delta ACB\) vuông tại C có \(CH\bot AB\Rightarrow AC^2=AH.AB\) (hệ thức lượng)
Xét \(\Delta AEH\) và \(\Delta ABM:\) Ta có: \(\left\{{}\begin{matrix}\angle AHE=\angle AMB=90\\\angle MABchung\end{matrix}\right.\)
\(\Rightarrow\Delta AEH\sim\Delta ABM\left(g-g\right)\Rightarrow\dfrac{AE}{AB}=\dfrac{AH}{AM}\Rightarrow AE.AM=AH.AB\)
\(\Rightarrow AE.AM=AC^2\Rightarrow\dfrac{AE}{AC}=\dfrac{AC}{AM}\)
Xét \(\Delta ACE\) và \(\Delta AMC:\) Ta có: \(\left\{{}\begin{matrix}\dfrac{AE}{AC}=\dfrac{AC}{AM}\\\angle MACchung\end{matrix}\right.\)
\(\Rightarrow\Delta ACE\sim\Delta AMC\left(c-g-c\right)\Rightarrow\dfrac{AE}{AC}=\dfrac{CE}{CM}\Rightarrow AE.CM=AC.EC\)


a, HS tự chứng minh
b, HS tự chứng minh
c, DAEH vuông nên ta có: KE = KA = 1 2 AH
=> DAKE cân tại K
=> K A E ^ = K E A ^
DEOC cân ở O => O C E ^ = O E C ^
H là trực tâm => AH ^ BC
Có A E K ^ + O E C ^ = H A C ^ + A C O ^ = 90 0
(K tâm ngoại tiếp) => OE ^ KE
d, HS tự làm
a) Ta thấy ^AMB chắn nửa đường tròn (O) đường kính AB nên ^AMB = 900
Khi đó tứ giác EHBM có ^EMB + ^EHB = 900 + 900 = 1800 => Tứ giác EHBM nội tiếp (đpcm).
b) Tương tự câu a thì ^ACB = 900 => \(\Delta\)ABC vuông tại C có đường cao CH
=> AC2 = AH.AB (Hệ thức lượng trong tam giác vuông) (đpcm).
Có ^ACE = ^ACH = ^ABC (Cùng phụ ^BCH) = ^AMC (2 góc nội tiếp cùng chắn cung AC)
Xét \(\Delta\)AEC và \(\Delta\)ACM: ^ACE = ^AMC (cmt), ^CAE = ^MAC (góc chung)
=> \(\Delta\)AEC ~ \(\Delta\)ACM (g.g) => \(\frac{AC}{AM}=\frac{CE}{MC}\)=> AC.MC = AM.CE (đpcm).
c) Gọi I là tâm ngoại tiếp của \(\Delta\)CEM. Trước hết ta chỉ ra điểm I thuộc đường thẳng BC.
Thật vậy: Vì (I) ngoại tiếp \(\Delta\)CEM nên \(\Delta\)EIC cân tại I
=> ^ICE = 900 - ^EIC/2 = 900 - ^EMC = 900 - ^ABC = ^HCB = ^ECB
Do I,B nằm cùng phía so với CE nên hai tia CI,CB trùng nhau hay B,I,C thẳng hàng
Khi đó điểm I di chuyển trên đường thẳng BC. Gọi HP vuông góc BC tại P
Vì khoảng cách từ H đến I là IH nên HI < HP. Do C,B,H cố định nên HP không đổi
Vậy Max IH = HP = const.
Cách dựng điểm M thỏa mãn đề:
B1: Dựng HI vuông góc với BC tại I
B2: Vẽ đường tròn tâm I bán kính IC cắt (O) và CH lần lượt tại M0 và E
Lúc này, I là tâm ngoại tiếp của tam giác CEM và M0 là điểm M cần tìm.
Sửa: IH > HP và Min IH = PH = const. Mình nhầm dấu chút xíu :D