Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B
+ Mức cường độ âm tại điểm M là trung điểm của AB được xác định bởi:
L M = 10 log P I 0 4 π S M 2 ↔ log P 10 - 12 4 π . 70 2 → P = 6 , 2 . 10 - 4 W.
→ Năng lượng giới hạn bởi hai mặt cầu E = P t = P A B v = 6 , 2 . 10 - 4 100 340 = 1 , 81 . 10 - 4 J.

Đáp án C
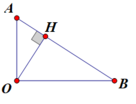
Công thức chung cho điểm M cách nguồn O 1 đoạn MO: I M = P 4 π M O 2 = I 0 .10 L M
Áp dụng công thức với:
+ Điểm A: khi có 1 nguồn âm: P 4 π A O 2 = I 0 .10 3
+ Điểm B: khi có 1 nguồn âm: P 4 π B O 2 = I 0 .10 L B
+ Điểm H: (chân đường vuông góc kẻ từ O đến AB) đây là điểm có mức cường độ âm lớn nhất vì gần nguồn nhất. Có 64 P 4 π H O 2 = I 0 .10 5
Có tam giác OAB vuông tại O, OH vuông góc AB
=> 1 O H 2 = 1 O A 2 + 1 O B 2 ⇒ 10 3 + 10 L B = 10 5 64 ⇒ L B = 2 , 75 ( B )

Công suất của nguồn: \(P=I.4\pi d^2=I_0.10^{\frac{L}{10}}.4\pi d^2=10^{-12}.10^{\frac{60}{10}}.4\pi.70^2=196\pi.10^{-4}\)(W)
Công suất này có nghĩa, trong 1 s có năng lượng là P (J) xuyên qua các mặt cầu đồng tâm S.
Như vậy, năng lượng trong vùng không gian giời hạn bởi hai mặt cầu tâm S qua A và B là: Q = P.t
trong đó t là thời gian sóng âm truyền từ A --> B: \(t=\frac{AB}{v}\)
\(\Rightarrow Q=196\pi.10^{-4}.\frac{100}{340}=0,0181J=18,1mJ\)
Đáp án D.





Đáp án D.
Năng lượng sóng âm từ nguồn điểm O khi truyền đi trong không gian sẽ phân bố đều cho các điểm nằm trên diện tích của mặt cầu tâm O, bán kính R. Vì vậy năng lượng sóng tại một điểm cách nguồn khoảng R tỉ lệ nghịch với bình phương khoảng cách tới nguồn, tỉ lệ thuận với bình phương biên độ dao động tại điểm đó
Do đó biên độ sóng tại điểm cách nguồn khoảng R tỉ lệ nghịch với R.
Gọi R A , R B lần lượt là khoảng cách từ các điểm A và B tới nguồn O, ta có:
Mặt khác
Thời gian sóng truyền từ A sang B là
Năng lượng sóng trong vùng không gian giới hạn bởi hai mặt cầu là: