
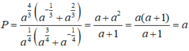
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

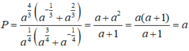

a) =
=
b) =
=
=
. ( Với điều kiện b # 1)
c) \(\dfrac{a^{\dfrac{1}{3}}b^{-\dfrac{1}{3}-}a^{-\dfrac{1}{3}}b^{\dfrac{1}{3}}}{\sqrt[3]{a^2}-\sqrt[3]{b^2}}\)= =
=
( với điều kiện a#b).
d) \(\dfrac{a^{\dfrac{1}{3}}\sqrt{b}+b^{\dfrac{1}{3}}\sqrt{a}}{\sqrt[6]{a}+\sqrt[6]{b}}\) = =
=
=

Câu a, b thì Nguyễn Quang Duy làm đúng rồi.
c) \(a^{\dfrac{4}{3}}:\sqrt[3]{a}=a^{\dfrac{4}{3}}:a^{\dfrac{1}{3}}=a^{\dfrac{4}{3}-\dfrac{1}{3}}=a\)
d) \(\sqrt[3]{b}:b^{\dfrac{1}{6}}=b^{\dfrac{1}{3}}:b^{\dfrac{1}{6}}=b^{\dfrac{1}{3}-\dfrac{1}{6}}=b^{\dfrac{1}{6}}\)

à:::::::::: a,b nguyên dương
\(S=8b^2+3b+8\)
vậy min S tại b=1 (số nguyên dương ) ......nhìn thôi cũng thấy rồi !
=>minS=19======>>>(B)
\(y'=\left(a-4\right)x^2+4bx+1\)
Để hàm số đồng biến trên R thì
\(\left\{{}\begin{matrix}a-4>0\\4b^2-\left(a-4\right)\le0\end{matrix}\right.\)
<=>\(\left\{{}\begin{matrix}a>4\\a-4\ge4b^2\end{matrix}\right.\)
ta thấy S=2a+3b nhỏ nhất khi a và b nhỏ nhất
ta thấy :\(a-4\ge4b^2\)
a và b sẽ mang giá trị nhỏ nhất khi \(a-4=4b^2\)
=>\(a=4b^2+4\)
vậy \(S=2\left(4b^2+4\right)+3b\)
vậy min S là : ...................
..............................
.................................
....................
\(-\infty\)
sao kì vậy ! may be lí luận sai chỗ nào đấy

a)
\(A=\dfrac{a^{\dfrac{4}{3}}\left(a^{-\dfrac{1}{3}}+a^{\dfrac{2}{3}}\right)}{a^{\dfrac{1}{4}}\left(a^{\dfrac{3}{4}}+a^{-\dfrac{1}{4}}\right)}=\dfrac{a^{\left(\dfrac{4}{3}-\dfrac{1}{3}\right)+}a^{\left(\dfrac{4}{3}+\dfrac{2}{3}\right)}}{a^{\left(\dfrac{1}{4}+\dfrac{3}{4}\right)}+a^{\left(\dfrac{1}{4}-\dfrac{1}{4}\right)}}=\dfrac{a+a^2}{a+1}=\dfrac{a\left(a+1\right)}{a+1}\)
\(a>0\Rightarrow a+1\ne0\) \(\Rightarrow A=a\)

Lời giải:
Ta có \(A=\frac{a^{\frac{1}{3}}-a^{\frac{7}{3}}}{a^{\frac{1}{3}}-a^{\frac{4}{3}}}-\frac{a^{\frac{1}{3}}-a^{\frac{5}{3}}}{a^{\frac{2}{3}}+a^{\frac{1}{3}}}\)
\(=\frac{\sqrt[3]{a}-\sqrt[3]{a^7}}{\sqrt[3]{a}-\sqrt[3]{a^4}}-\frac{\sqrt[3]{a}-\sqrt[3]{a^5}}{\sqrt[3]{a^2}+\sqrt[3]{a}}\)
\(=\frac{\sqrt[3]{a}(1-a^2)}{\sqrt[3]{a}(1-a)}-\frac{\sqrt[3]{a}(1-\sqrt[3]{a^4})}{\sqrt[3]{a}(1+\sqrt[3]{a})}=\frac{1-a^2}{1-a}-\frac{1-\sqrt[3]{a^4}}{1+\sqrt[3]{a}}\)
\(=1+a-\frac{1-\sqrt[3]{a^4}}{1+\sqrt[3]{a}}\)
Đặt \(\sqrt[3]{a}=t\Rightarrow A=1+t^3-\frac{1-t^4}{1+t}=1+t^3-\frac{(1-t^2)(1+t^2)}{1+t}\)
\(=1+t^3-\frac{(1-t)(1+t)(1+t^2)}{1+t}=1+t^3-(1-t)(1+t^2)\)
\(=2t^3-t^2+t\)

a;b phải thỏa mãn hệ điều kiện \(\left\{{}\begin{matrix}a>4\\4b^2-a+4\le0\end{matrix}\right.\) mà bạn
Nếu a=5 thì ko có b nguyên dương thỏa mãn điều kiện delta bên dưới
Do đó cần rút a từ điều kiện delta: \(a\ge4b^2+4\) thay vào S và khảo sát hàm bậc 2 \(f\left(b\right)\)
Đồng thời b nguyên dương nên khi a thỏa mãn \(a\ge4b^2+4\) thì cũng hiển nhiên thỏa mãn luôn a>4
\(y'=\left(a-4\right)x^2+4bx+1\)
Do hàm số đồng biến trên R \(\Leftrightarrow\left\{{}\begin{matrix}a-4>0\\\Delta'=4b^2-a+4\le0\end{matrix}\right.\)
\(\Rightarrow a\ge4b^2+4\)
\(\Rightarrow S=2a+3b\ge2\left(4b^2+4\right)+3b\)
\(\Rightarrow S=f\left(b\right)\ge8b^2+3b+8\)
\(f\left(b\right)\) đồng biến khi \(b\) dương \(\Rightarrow f\left(b\right)_{min}\) khi \(b=1\Rightarrow S_{min}=19\) khi \(\left\{{}\begin{matrix}a=8\\b=1\end{matrix}\right.\)