Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

góc moz= 1/2 góc xoz(1) ( vÌ om là p/g của xoz)
gÓC noz= 1/2 góc yoz (2) ( vÌ on là tia p/g của góc yoz)
tu (1) va (2) ta co : moz + noz = 1/2xoz +1/2 yoz
moz + noz = 1/2 ( xỏr + yoz)
moz + noz = 1/2. 180 Đo
moz + noz = 90 do
chuppy moe sao lại là moz và noz người ta cho aob va aoc mà bạn giải thích giúp mình

Do mình không biết vẽ hình như nào nên mình sẽ chỉ giải bài thôi nhé , thoog cảm
Bài 1
Ta có \(\widehat{AOC}+\widehat{BOD}+\widehat{COD}=120^0\)
hay \(30^o+30^o+\widehat{COD}=120^o\)
\(\Rightarrow\widehat{COD}=120^o-30^o-30^o=60^o\)
Mà \(\widehat{AOC}+\widehat{COD}=30^o+60^o=90^o\)
Hay OA vuông góc với OD
Tương tự ta có OB vuông góc với OC
Vậy OA vuông góc với OD ; OB vuông góc với OC

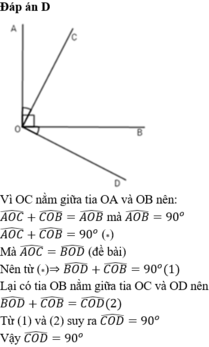
Ta có tia OC nằm trong góc AOB nên luôn có đẳng thức:
AOC+BOC=AOB=90
Theo đề bài thì AOC=BOD nên BOD+BOC=AOC+BOC=90
Nhưng chú ý rằng do OD nằm khác phía với OC qua OB nên hiển nhiên OB nằm trong COD
Cho nên BOC+BOD =COD
Do vậy COD=90 hay OC vuông góc với OD

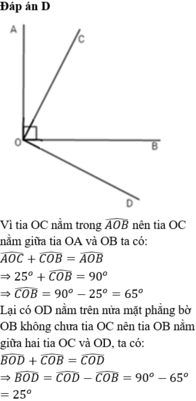
Tia Od thuộc nửa mặt phẳng bờ Ob không chứa Oc
=> Tia Ob nằm trong ^cOd
=> ^cOd = ^cOb + ^bOd = ^cOb + ^ aOc = ^aOb = 90 độ.
=> Tia Oc và tia Od vuông góc với nhau.
Ta có:
\(\widehat{AOB}=90^o\left(gt\right)\)
\(\widehat{AOC}=\widehat{BOD}\) (gt)
\(\Rightarrow\) \(\widehat{AOB}=\widehat{AOC}+\widehat{COB}=\widehat{BOD}+\widehat{COB}=90^O\) hay OC \(\perp\) OD