Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bạn coi lại đề, SA vuông góc AD hay SA vuông góc (ABCD)
Nếu SA chỉ vuông góc AD thì không thể chứng minh CD vuông góc SD

a.
\(SA\perp\left(ABCD\right)\Rightarrow AB\) là hình chiếu vuông góc của SB lên (ABCD)
\(\Rightarrow\widehat{SBA}=\left(SB;\left(ABCD\right)\right)\)
\(tan\widehat{SBA}=\dfrac{SA}{AB}=\dfrac{\sqrt{2}}{2}\Rightarrow\widehat{SBA}\approx35^016'\)
Tương tự \(SA\perp\left(ABCD\right)\Rightarrow\widehat{SCA}=\left(SC;\left(ABCD\right)\right)\)
\(AC=\sqrt{AD^2+DC^2}=a\sqrt{2}\)
\(\Rightarrow tan\widehat{SCA}=\dfrac{SA}{AC}=1\Rightarrow\widehat{SCA}=45^0\)
b.
\(\left\{{}\begin{matrix}SA\perp\left(ABCD\right)\Rightarrow SA\perp AB\\AB\perp AD\end{matrix}\right.\) \(\Rightarrow AB\perp\left(SAD\right)\)
\(\Rightarrow\left(AH;\left(SAD\right)\right)=90^0-\left(AH;AB\right)=90^0-\widehat{HAB}\)
Gọi E là trung điểm AB \(\Rightarrow ADCE\) là hình vuông \(\Rightarrow\widehat{ACE}=45^0\)
Tam giác BCE vuông cân tại E (do \(EB=EC=a\)) nên \(\widehat{ECB}=45^0\)
\(\Rightarrow\widehat{ACB}=90^0\) hay \(BC\perp AC\Rightarrow BC\perp\left(SAC\right)\) (do \(SA\perp BC\))
\(\Rightarrow BC\perp AH\Rightarrow AH\perp\left(SBC\right)\Rightarrow AH\perp BH\)
Hay tam giác ABH vuông tại H
\(AH=\dfrac{SA.AC}{\sqrt{SA^2+AC^2}}=a\)
\(\Rightarrow cos\widehat{HAB}=\dfrac{AH}{AB}=\dfrac{1}{2}\Rightarrow\widehat{HAB}=60^0\)
\(\Rightarrow\widehat{HAB}=60^0\Rightarrow\left(AH;\left(SAD\right)\right)=30^0\)
Theo cmt \(BC\perp\left(SAC\right)\Rightarrow\left(SB;\left(SAC\right)\right)=\widehat{BSC}\)
\(SC=\sqrt{SA^2+AC^2}=2a\) ; \(SB=\sqrt{SA^2+AB^2}=a\sqrt{6}\)
\(\Rightarrow cos\widehat{BSC}=\dfrac{SC}{SB}=\dfrac{\sqrt{6}}{3}\Rightarrow\widehat{BSC}\approx35^016'\)

a: BC vuông góc SA
BC vuông góc AB
=>CB vuông góc (SBA)
DC vuông góc AD
DC vuông góc SA
=>DC vuông góc (SAD)
=>(SDC) vuông góc (SAD)
b: (SC;(SAD))=(SC;SD)=góc CSD
\(SD=\sqrt{SA^2+AD^2}=2a\sqrt{7}\)
\(AC=\sqrt{\left(2a\right)^2+3a^2}=a\sqrt{7}\)
\(SC=\sqrt{SA^2+AC^2}=4a\sqrt{2}\)
\(cosCSD=\dfrac{SC^2+SD^2-DC^2}{2\cdot SC\cdot SD}=\dfrac{32a^2+28a^2-4a^2}{2\cdot2a\sqrt{7}\cdot4a\sqrt{2}}=\dfrac{\sqrt{14}}{4}\)
=>góc CSD=21 độ
(SC;(ABCD))=(CS;CA)=góc SCA
tan SCA=SA/AC=5/căn 7
=>góc SCA=62 độ

a: BC vuông góc AB; BC vuông góc SA
=>BC vuông góc (SAB)
b: (BS;(BACD))=(BS;BA)=góc SBA
tan SBA=SA/AB=căn 5/2
=>góc SBA=48 độ
(SC;(ABCD))=(CS;CA)=góc SCA
tan SCA=SA/AC=1
=>góc SCA=45 độ

\(\left\{{}\begin{matrix}SA\perp\left(ABCD\right)\Rightarrow SA\perp BC\\AB\perp BC\end{matrix}\right.\) \(\Rightarrow BC\perp\left(SAB\right)\)
\(\left\{{}\begin{matrix}SA\perp\left(ABCD\right)\Rightarrow SA\perp CD\\CD\perp AD\end{matrix}\right.\) \(\Rightarrow CD\perp\left(SAD\right)\)
\(\left\{{}\begin{matrix}SA\perp\left(ABCD\right)\Rightarrow SA\perp AC\\BD\perp AC\left(\text{hai đường chéo hình vuông}\right)\end{matrix}\right.\) \(\Rightarrow BD\perp\left(SAC\right)\)
\(BC\perp\left(SAB\right)\Rightarrow BC\perp AH\) ; mà \(AH\perp SB\Rightarrow AH\perp\left(SBC\right)\)
\(\left\{{}\begin{matrix}CD\perp\left(SAD\right)\Rightarrow CD\perp AK\\AK\perp SD\end{matrix}\right.\) \(\Rightarrow AK\perp\left(SCD\right)\)
\(\left\{{}\begin{matrix}AH\perp\left(SBC\right)\Rightarrow AH\perp SC\\AK\perp\left(SCD\right)\Rightarrow AK\perp SC\end{matrix}\right.\) \(\Rightarrow SC\perp\left(AHK\right)\Rightarrow SC\perp HK\)
Mặt khác theo tính đối xứng hình vuông \(\Rightarrow HK||BD\Rightarrow HK\perp AC\Rightarrow HK\perp\left(SAC\right)\)
\(AI\in\left(SAC\right)\Rightarrow HK\perp AI\)
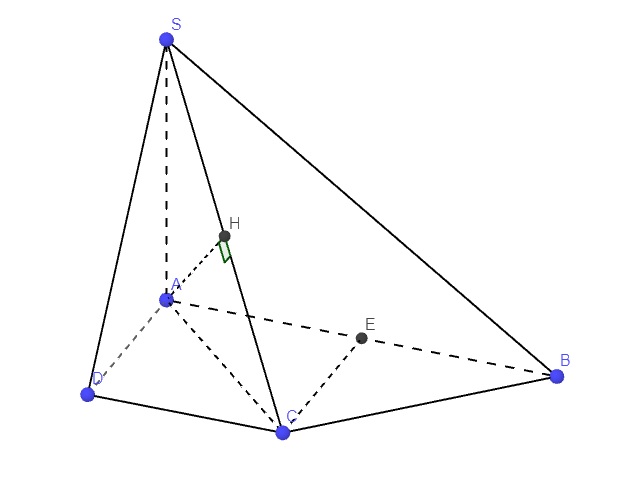
Đề bài sai rồi bạn, AB thuộc (SAB) nên không thể vuông góc (SAB)
Tương tự AD thuộc (SAD) nên AD không thể vuông góc (SAD)
Chỉ có thể là AB vuông góc (SAD), AD vuông góc (SAB)