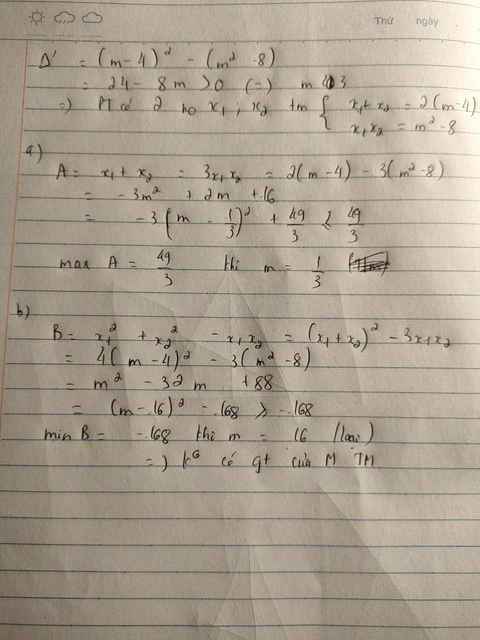Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Áp dụng hệ thức Vi-ét,ta có : \(\hept{\begin{cases}x_1+x_2=-2\left(m-1\right)\\x_1x_2=4m\end{cases}}\)
Ta có : \(4x_1^2\left(1+x_2\right)+4x_2\left(1+x_1\right)+x_1^2x_2^2=36\)
\(\Rightarrow4\left(x_1^2+x_2^2\right)+4x_1x_2\left(x_1+x_2\right)+x_1^2x_2^2=36\)
\(\Rightarrow4\left[\left(x_1+x_2\right)^2-2x_1x_2\right]+4x_1x_2\left(x_1+x_2\right)+x_1^2x_2^2=36\)
thay vào rồi tìm m thôi

\(\Delta'=\left(-2\right)^2-3.\left(-8\right)=4+24=28>0.\)
\(\Rightarrow\) Pt có 2 nghiệm phân biệt \(x_1;x_2.\)
\(\Rightarrow\left\{{}\begin{matrix}x_1=\dfrac{2+2\sqrt{7}}{3}.\\x_2=\dfrac{2-2\sqrt{7}}{3}.\end{matrix}\right.\)

\(\Delta=\left(m-2\right)^2+8>0\) với mọi m . Vậy pt có 2 nghiệm phân biệt với mọi m
Do : \(x_1x_2=-8\) nên \(x_2=\dfrac{-8}{x1}\)
\(Q=\left(x_1^2-1\right)\left(x_2^2-4\right)=\left(x_1^2-1\right)\left(\dfrac{64}{x_1^2}-4\right)=68-4\left(x_1^2+\dfrac{16}{x_1^2}\right)\le68-4.8=36\)
\(\left(x_1^2+\dfrac{16}{x_1^2}\ge8\right)\)\(;Q=36\) khi và chỉ khi x1 = ( 2 ; -2 )

Ta có: \(\frac{c}{a}=-\frac{2}{2}=-1< 0\)
=> Phương trình luôn có 2 ngiệm trái dấu \(x_1;x_2\)
Theo định lí viet: \(x_1x_2=-1;x_1+x_2=\frac{1-m}{2}\)
Ta có: \(\left(x_1+\frac{1}{2}x^2_1-x^3_1\right)\left(x_2+\frac{1}{2}x^2_2-x^3_2\right)=4\)
<=> \(x_1x_2\left(x_1^2-\frac{1}{2}x_1-1\right)\left(x_2^2-\frac{1}{2}x_2-x_2\right)=4\)
<=> \(\left(2x_1^2-x_1-2\right)\left(2x_2^2-x_2-2\right)=-16\)
<=> \(\left(2x_1x_2\right)^2-2x_1^2x_2-4x_1^2-2x_1x_2^2+x_1x_2+2x_2-4x_2^2+2x_2+4=-16\)
<=> \(4+2x_1-4x_1^2+2x_2-1+2x_2-4x_2^2+2x_2+4=-16\)
<=> \(4x_1^2+4x_2^2-4x_1-4x_2=23\)
<=> \(4\left(x_1+x_2\right)^2-4\left(x_1+x_2\right)=15\)
<=> \(\orbr{\begin{cases}x_1+x_2=\frac{5}{2}\\x_1+x_2=-\frac{3}{2}\end{cases}}\Leftrightarrow\orbr{\begin{cases}\frac{1-m}{2}=\frac{5}{2}\\\frac{1-m}{2}=-\frac{3}{2}\end{cases}}\Leftrightarrow\orbr{\begin{cases}m=-4\\m=4\end{cases}}\)
Vậy:....

\(\Delta'=\left[-\left(m+4\right)\right]^2-1\left(m^2-8\right)=m^2+8m+16-m^2+8=8m+24\)
Để pt có 2 nghiệm thì \(\Delta'\ge0\Leftrightarrow8m+24\ge0\Leftrightarrow m\ge-3\)
Áp dụng định lý Vi-ét ta có:\(\left\{{}\begin{matrix}x_1+x_2=2m+8\\x_1x_2=m^2-8\end{matrix}\right.\)
\(A=x^2_1+x^2_2-x_1-x_2\\ =\left(x_1+x_2\right)^2-2x_1x_2-\left(x_1+x_2\right)\\ =\left(2m+8\right)^2-2\left(m^2-8\right)-\left(2m+8\right)\\ =4m^2+32m+64-2m^2+16-2m-16\\ =2m^2+30m+64\)
Amin=\(-\dfrac{97}{2}\)\(\Leftrightarrow m=-\dfrac{15}{2}\)
\(B=x^2_1+x^2_2-x_1x_2\\ =\left(x_1+x_2\right)^2-3x_1x_2\\ =\left(2m+8\right)^2-3\left(m^2-8\right)\\ =4m^2+32m+64-3m^2+24\\ =m^2+32m+88\)
Bmin=-168\(\Leftrightarrow\)m=-16