Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a:Sửa đề: x^2-(m+1)x+2m-8=0
Khi m=2 thì (1) sẽ là x^2-3x-4=0
=>(x-4)(x+1)=0
=>x=4 hoặc x=-1
b: Δ=(-m-1)^2-4(2m-8)
=m^2+2m+1-8m+32
=m^2-6m+33
=(m-3)^2+24>=24>0
=>(1) luôn có hai nghiệm pb
\(x_1^2+x_2^2+\left(x_1-2\right)\left(x_2-2\right)=11\)
=>(x1+x2)^2-2x1x2+x1x2-2(x1+x2)+4=11
=>(m+1)^2-(2m-8)-2(m+1)+4=11
=>m^2+2m+1-2m+8-2m-2+4=11
=>m^2-2m=0
=>m=0 hoặc m=2

\(\Delta'=1-4\left(m+1\right)=-4m-3>0\Rightarrow m< -\dfrac{3}{4}\)
Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=1\\x_1x_2=m+1\end{matrix}\right.\)
\(x_1^2+x_1x_2=7-3x_2\)
\(\Leftrightarrow x_1\left(x_1+x_2\right)=7-3x_2\)
\(\Leftrightarrow x_1=7-3x_2\)
\(\Leftrightarrow x_1+x_2=7-2x_2\)
\(\Leftrightarrow1=7-2x_2\Rightarrow x_2=3\Rightarrow x_1=1-x_2=-2\)
Thế vào \(x_1x_2=m+1\Rightarrow-6=m+1\Rightarrow m=-7\)

Theo định lý Vi-ét, ta có:
\(\left\{{}\begin{matrix}x_1+x_2=2\left(m+1\right)\\x_1.x_2=2m-2\end{matrix}\right.\)
Ta có: \(x_1^2+2\left(m+1\right)x_2+2m-2\)\(=x1^2+x_1+x_2.x_2+x_1.x_2\)
\(=x_1^2+2x_1x_2+x_2^2=\left(x_1+x_2\right)^2\) \(=\left[2\left(m+1\right)\right]^2=4\left(m+1\right)^2\)
Ta có: \(4\left(m+1\right)^2=9\Leftrightarrow\left(m+1\right)^2=\dfrac{9}{4}\) \(\Leftrightarrow\left[{}\begin{matrix}m+1=\dfrac{3}{2}\\m+1=\dfrac{-3}{2}\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}m=\dfrac{1}{2}\\m=\dfrac{-5}{2}\end{matrix}\right.\)
Vậy \(m=\dfrac{1}{2};m=\dfrac{-5}{2}\) thoả mãn yêu cầu đề bài
Dấu bằng thứ nhất sau chữ ta có đầu tiên sửa thành: \(x_1^2+\left(x_1+x_2\right).x_2+x_1x_2\)
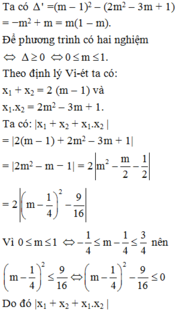
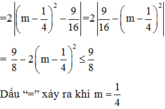
à đây là lớp 9 mà mình tưởng lớp 6 !??