Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

ĐKXĐ: ...
\(\Leftrightarrow m^2+m\left(x^2-3x-4\right)-m\sqrt{x+7}-\left(x^2-3x-4\right)\sqrt{x+7}=0\)
\(\Leftrightarrow m\left(x^2-3x-4+m\right)-\sqrt{x+7}\left(x^2-3x-4+m\right)=0\)
\(\Leftrightarrow\left(m-\sqrt{x+7}\right)\left(x^2-3x-4+m\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}m=\sqrt{x+7}\left(1\right)\\m=-x^2+3x+4\left(2\right)\end{matrix}\right.\)
Với \(m\) nguyên tố \(\Rightarrow\) (1) luôn có đúng 1 nghiệm
Để pt có số nghiệm nhiều nhất \(\Rightarrow\) (2) có 2 nghiệm pb
\(\Rightarrow y=m\) cắt \(y=-x^2+3x+4\) tại 2 điểm pb thỏa mãn \(x\ge-7\)
\(\Rightarrow-66\le m\le\dfrac{25}{4}\Rightarrow m=\left\{2;3;5\right\}\)

ĐK: \(-3\le x\le6\)
Đặt \(\sqrt{x+3}+\sqrt{6-x}=t\left(3\le t\le3\sqrt{2}\right)\)
\(\Rightarrow\sqrt{\left(x+3\right)\left(6-x\right)}=\dfrac{t^2-9}{2}\)
\(\sqrt{x+3}+\sqrt{6-x}-\sqrt{\left(x+3\right)\left(6-x\right)}=m\)
\(\Leftrightarrow m=f\left(t\right)=\dfrac{-t^2+2t+9}{2}\)
Yêu cầu bài toán thỏa mãn khi \(minf\left(t\right)\le m\le maxf\left(x\right)\)
\(\Leftrightarrow\dfrac{-9+6\sqrt{2}}{2}\le m\le3\)

ĐKXĐ: \(-3\le x\le6\)
Đặt \(\sqrt{x+3}+\sqrt{6-x}=t\)
Ta có: \(t=\sqrt{x+3}+\sqrt{6-x}\ge\sqrt{x+3+6-x}=3\)
\(t\le\sqrt{2\left(x+3+6-x\right)}=3\sqrt{2}\)
\(\Rightarrow3\le t\le3\sqrt{2}\)
Lại có:
\(t^2=9+2\sqrt{\left(x+3\right)\left(6-x\right)}\Rightarrow-\sqrt{\left(x+3\right)\left(6-x\right)}=\dfrac{9-t^2}{2}\)
Phương trình trở thành:
\(t+\dfrac{9-t^2}{2}=m\Leftrightarrow m=-\dfrac{1}{2}t^2+t+\dfrac{9}{2}\)
Xét hàm \(f\left(t\right)=-\dfrac{1}{2}t^2+t+\dfrac{9}{2}\) trên \(\left[3;3\sqrt{2}\right]\)
\(-\dfrac{b}{2a}=1\notin\left[3;3\sqrt{2}\right]\)
\(f\left(3\right)=3\) ; \(f\left(3\sqrt{2}\right)=\dfrac{-9+6\sqrt{2}}{2}\)
\(\Rightarrow\dfrac{-9+6\sqrt{2}}{2}\le f\left(t\right)\le3\)
\(\Rightarrow\) Phương trình có nghiệm khi \(\dfrac{-9+6\sqrt{2}}{2}\le m\le3\)
Có 4 giá trị nguyên của m thỏa mãn

Điều kiện xác định x∈Rx∈R.
Đặt t=√x2+1 (t≥1t≥1)
Phương trình trở thành t2−1−4t−m+1=0
⇔t2−4t=m
⇔t2−4t=m. (1)
Để phương trình có 44 nghiệm phân biệt thì phương trình (1) có hai nghiệm phân biệt lớn hơn 11.
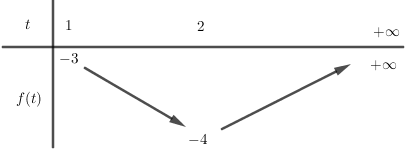
Xét hàm số f(t)=t2−4t có đồ thị là parabol có hoành độ đỉnh x=2∈(1;+∞) nên ta có bảng biến thiên:
Dựa BBT ta thấy để (1) có hai nghiệm phân biệt lớn hơn 11 thì −4<m<−3
Vậy không có giá trị nguyên của mm thỏa mãn yêu cầu bài toán.

ĐKXĐ: \(x\ge0\)
- Với \(x=0\) không phải nghiệm
- Với \(x>0\) , chia 2 vế của pt cho \(x\) ta được:
\(\dfrac{4x^2+1}{x}+2\sqrt{\dfrac{4x^2+1}{x}}+3-2m=0\)
Đặt \(t=\sqrt{\dfrac{4x^2+1}{x}}\ge\sqrt{\dfrac{2\sqrt{4x^2}}{x}}=2\)
Pt trở thành: \(t^2+2t+3-2m=0\)
\(\Leftrightarrow t^2+2t+3=2m\) (1)
Pt đã cho có nghiệm khi và chỉ khi (1) có nghiệm \(t\ge2\)
Xét hàm \(f\left(t\right)=t^2+2t+3\) khi \(t\ge2\)
Do \(\left\{{}\begin{matrix}a=1>0\\-\dfrac{b}{2a}=-1< 2\end{matrix}\right.\) \(\Rightarrow f\left(t\right)\) đồng biến khi \(t\ge2\)
\(\Rightarrow f\left(t\right)\ge f\left(2\right)=11\)
\(\Rightarrow\) Pt có nghiệm khi \(2m\ge11\Rightarrow m\ge\dfrac{11}{2}\)

ĐKXĐ: \(x\ge0\)
\(x^2+1+\left(2-m\right)x-2\sqrt{x\left(x^2+1\right)}=0\)
Với \(x=0\) ko phải nghiệm, với \(x>0\) chia 2 vế cho x:
\(\Rightarrow\dfrac{x^2+1}{x}+2-m-2\sqrt{\dfrac{x^2+1}{x}}=0\)
Đặt \(\sqrt{\dfrac{x^2+1}{x}}=t\ge\sqrt{2}\)
\(\Rightarrow t^2-2t+2=m\)
Xét hàm \(f\left(t\right)=t^2-2t+m\) khi \(t\ge\sqrt{2}\)
\(\left\{{}\begin{matrix}a=1>0\\-\dfrac{b}{2a}=1< \sqrt{2}\end{matrix}\right.\) \(\Rightarrow f\left(t\right)\) đồng biến khi \(t\ge\sqrt{2}\)
\(\Rightarrow f\left(t\right)\ge f\left(\sqrt{2}\right)=4-2\sqrt{2}\)
\(\Rightarrow\) Pt có nghiệm khi \(m\ge4-2\sqrt{2}\)

Phương trình đã cho tương đương
\(\left\{{}\begin{matrix}x\in\left[2;10\right];x\ge\dfrac{m-3}{3}\\\left[{}\begin{matrix}x=4\\x=-1\\x=11\end{matrix}\right.\end{matrix}\right.\)
Để phương trình có 2 nghiệm phân biệt thì
\(\left[{}\begin{matrix}x=4\\x=-1\\x=10\end{matrix}\right.\) không thỏa mãn điều kiện x ≥ \(\dfrac{m-3}{3}\)
⇔ \(\left[{}\begin{matrix}4< \dfrac{m-3}{3}\\-1< \dfrac{m-3}{3}\\10< \dfrac{m-3}{3}\end{matrix}\right.\)
⇔ \(\left[{}\begin{matrix}m>15\\m>0\\m>33\end{matrix}\right.\) . (1)
Dựa vào trục số, (1) ⇔ m > 0
Vậy điều kiện của m là m > 0
Sai thì thứ lỗi ạ !

\(\Leftrightarrow2m.2^x+\left(2m+1\right)\left(3-\sqrt{5}\right)^x+\left(3+\sqrt{5}\right)^x=0\)
\(\Leftrightarrow\left(\frac{3+\sqrt{5}}{2}\right)^x+\left(2m+1\right)\left(\frac{3-\sqrt{5}}{2}\right)^x+2m< 0\)
Đặt \(t=\left(\frac{3+\sqrt{5}}{2}\right)^x,0< t\le1\Rightarrow\frac{1}{t}=\left(\frac{3-\sqrt{5}}{2}\right)^x\)
Phương trình trở thành :
\(t+\left(2m+1\right)\frac{1}{t}+2m=0\) (*)
a. Khi \(m=-\frac{1}{2}\) ta có \(t=1\) suy ra \(\left(\frac{3+\sqrt{5}}{2}\right)^x=1\Leftrightarrow x=0\)
Vậy phương trình có nghiệm là \(x=0\)
b. Phương trình (*) \(\Leftrightarrow t^2+1=-2m\left(t+1\right)\Leftrightarrow\frac{t^2+1}{t+1}=-2m\)
Xét hàm số \(f\left(t\right)=\frac{t^2+1}{t+1};t\in\)(0;1]
Ta có : \(f'\left(t\right)=\frac{t^2+2t+1}{\left(t+1\right)^2}\Rightarrow f'\left(t\right)=0\Leftrightarrow=-1+\sqrt{2}\)
Suy ra phương trình đã cho có nghiệm đúng
\(\Leftrightarrow2\sqrt{2}-2\le-2m\le1\Leftrightarrow\sqrt{2}-1\ge m\ge-\frac{1}{2}\)
Vậy \(m\in\left[-\frac{1}{2};\sqrt{2}-1\right]\) là giá trị cần tìm
Đặt \(\sqrt{x-1}+\sqrt{5-x}=t\)
\(t\ge\sqrt{x-1+5-x}=2\)
\(t\le\sqrt{2\left(x-1+5-x\right)}=2\sqrt{2}\)
\(t^2=4+2\sqrt{\left(x-1\right)\left(5-x\right)}\Rightarrow\sqrt{\left(x-1\right)\left(5-x\right)}=\dfrac{t^2-4}{2}\)
Pt trở thành:
\(t+\dfrac{3\left(t^2-4\right)}{2}=m\Leftrightarrow\dfrac{3}{2}t^2+t-6=m\)
Xét hàm \(f\left(t\right)=\dfrac{3}{2}t^2+t-6\) với \(t\in\left[2;2\sqrt{2}\right]\)
\(-\dfrac{b}{2a}=-\dfrac{1}{3}\notin\left[2;2\sqrt{2}\right]\)
\(f\left(2\right)=2\) ; \(f\left(2\sqrt{2}\right)=6+2\sqrt{2}\) \(\Rightarrow2\le f\left(t\right)\le6+2\sqrt{2}\)
\(\Rightarrow\) Pt có nghiệm khi \(2\le m\le6+2\sqrt{2}\)
Anh ơi! Anh chỉ em tiếp ạ, em chưa hiểu cách suy điều kiện t của anh ạ, trước khi đặt t thì em điều kiện trong căn trước ạ!