Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
a: Ta có: \(\left(m-1\right)x^2-2x-m+1=0\)
a=m-1; b=-2; c=-m+1
\(ac=\left(m-1\right)\left(-m+1\right)=-\left(m-1\right)^2< 0\forall m\)
Do đó: Phương trình luôn có hai nghiệm trái dấu
b: \(x_1^2+x_2^2=6\)
\(\Leftrightarrow\left(x_1+x_2\right)^2-2x_1x_2=6\)
\(\Leftrightarrow\left(\dfrac{2}{m-1}\right)^2-2\cdot\dfrac{-m+1}{m-1}=6\)
\(\Leftrightarrow\dfrac{4}{\left(m-1\right)^2}=4\)
\(\Leftrightarrow\left(m-1\right)^2=1\)
=>m-1=1 hoặc m-1=-1
=>m=2 hoặc m=0
b) Theo hệ thức Vi ét ta có:
\(\left\{{}\begin{matrix}x_1+x_2=-\dfrac{2m-2}{m}\\x_1.x_2=\dfrac{m-1}{m}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x_1+x_2=\dfrac{2-2m}{m}\\x_1.x_2=\dfrac{m-1}{m}\end{matrix}\right.\)
Ta có:
\(Q=\dfrac{1013}{x_1}+\dfrac{1013}{x_2}+1=1013\left(\dfrac{1}{x_1}+\dfrac{1}{x_2}\right)+1\)
\(=1013\left(\dfrac{x_1+x_2}{x_1.x_2}\right)+1=1013\left(\dfrac{\dfrac{2-2m}{m}}{\dfrac{m-1}{m}}\right)+1\)
\(=1013.\dfrac{-2\left(m-1\right)}{m-1}+1=-2026+1=-2025\), luôn là hằng số (đpcm)
Phương trình đã cho nghiệm đúng với hay phương trình có vô số nghiệm khi
m 2 − 3 m + 2 = 0 − ( m 2 + 4 m + 5 ) = 0 ⇔ m = 1 m = 2 m ∈ ∅ ⇔ m ∈ ∅
Đáp án cần chọn là: D
Phương trình có 2 nghiệm x 1 , x 2 thỏa mãn x 1 + x 2 = 13 4
⇔ a ≠ 0 Δ ≥ 0 − b a = 13 4 ⇔ m ≠ 0 m 2 − 3 3 − 4 m 2 ≥ 0 − m 2 − 3 m = 13 4
⇔ m ≠ 0 m 2 − 3 − 2 m m 2 − 3 + 2 m ≥ 0 4 m 2 + 13 m − 12 = 0
⇔ m ≠ 0 m + 1 m − 3 m − 1 m + 3 ≥ 0 m = 3 4 ; m = − 4
⇔ m ≠ 0 m ∈ − ∞ ; − 3 ∪ − 1 ; 1 ∪ 3 ; + ∞ m = 3 4 ; m = − 4 ⇔ m = 3 4 m = − 4
Vậy tổng bình phương các giá trị của m là: 265 16
Đáp án cần chọn là: A
a:
\(\text{Δ}=\left(m-1\right)^2-4\left(-2m-1\right)\)
\(=m^2-2m+1+8m+4=m^2+6m+5\)
Để (1) vô nghiệm thì (m+1)(m+5)<0
hay -5<m<-1
Để (1) có nghiệm thì (m+1)(m+5)>=0
=>m>=-1 hoặc m<=-5
Để (1) có hai nghiệm phân biệt thì (m+1)(m+5)>0
=>m>-1 hoặc m<-5
b: Để (1) có hai nghiệm phân biệt cùng dương thì
\(\left\{{}\begin{matrix}\left[{}\begin{matrix}m>-1\\m< -5\end{matrix}\right.\\m>1\\m< -\dfrac{1}{2}\end{matrix}\right.\Leftrightarrow m\in\varnothing\)
c. Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=m-1\\x_1x_2=-2m-1\end{matrix}\right.\)
\(x_1^2+x_2^2=3\Leftrightarrow\left(x_1+x_2\right)^2-2x_1x_2=3\)
\(\Leftrightarrow\left(m-1\right)^2+2\left(2m+1\right)=3\)
\(\Leftrightarrow m^2+2m=0\Rightarrow\left[{}\begin{matrix}m=0\\m=-2\left(loại\right)\end{matrix}\right.\)
*Xét phương trình (m2 +1).x2 – (m- 6)x - 2= 0 có a= m2 + 1 >0 và c = -2 < 0 nên ac< 0 mọi m.
=> Phương trình (1) luôn có nghiệm mọi m.
* Phương trình x 2 + m + 3 x - 1 = 0 có ac= 1. (-1) < 0 nên phương trình này luôn có nghiệm mọi m.
* Xét (3) mx2 - 2x – m = 0 . Khi m= 0 thì (3) trở thành: - 2x = 0 đây là phương trình bậc nhất có nghiệm duy nhất là x = 0.
* Xét (4) có :
∆ = - 2 m 2 - 4 . 2 - 1 - m = 4 m 2 + 8 + 8 m = 4 m 2 + 8 m + 4 + 4 = 4 m + 1 2 + 4 > 0 ∀ m
Nên trình (4) luôn có 2 nghiệm phân biệt với mọi m.
Chọn C.
\(x^4-1-mx^2+m=0\)
\(\Leftrightarrow\left(x^2-1\right)\left(x^2+1\right)-m\left(x^2-1\right)=0\)
\(\Leftrightarrow\left(x^2-1\right)\left(x^2-m+1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x^2=1\\x^2=m-1\end{matrix}\right.\)
Pt có 4 nghiệm pb \(\Leftrightarrow\left\{{}\begin{matrix}m>1\\m\ne2\end{matrix}\right.\)
Khi đó ta có:
\(\left|x_1-x_2\right|=\left|1-\sqrt{m-1}\right|=1\)
\(\Leftrightarrow\left[{}\begin{matrix}1-\sqrt{m-1}=1\\1-\sqrt{m-1}=-1\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}m=1\left(loại\right)\\m=5\end{matrix}\right.\)
Vậy \(m_0=5\)
a) mx2 – 2x – 4m – 1 = 0 (1)
Với m ≠ 0, ta có:
Δ’ = 1 + m.(4m + 1) = 4m2 + m + 1
=
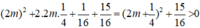với mọi m.
Hay phương trình (1) có hai nghiệm phân biệt với mọi m ≠ 0.
b) x = -1 là nghiệm của phương trình (1)
⇔ m.(-1)2 – 2.(-1) – 4m – 1 = 0
⇔ m + 2 - 4m = 0
⇔ -3m + 1 = 0
⇔ m = 1/3.
Vậy với m = 1/3 thì phương trình (1) nhận -1 là nghiệm.
Khi đó theo định lý Vi-et ta có: x2 + (-1) = 2/m (x2 là nghiệm còn lại của (1))
⇒ x2 = 2/m + 1= 6 + 1 = 7.
Vậy nghiệm còn lại của (1) là 7.