Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
a) Nếu Δ > 0 thì từ phương trình (2) suy ra x + b/2a = ± √Δ/2a
Do đó,phương trình (1) có hai nghiệm x 1 = ( - b + √ Δ ) / 2 a ; x 2 = ( - b - √ Δ ) / 2 a
b) Nếu Δ = 0 thì từ phương trình (2) suy ra ( x + b / 2 a ) 2 = 0
Do đó,phương trình (1) có nghiệm kép x = (-b)/2a
a) Phương trình x 2 – 2 ( m – 1 ) x + m 2 = 0 (1)
Có a = 1; b’ = -(m – 1); c = m 2
b) Phương trình (1):
+ Vô nghiệm ⇔ Δ’ < 0 ⇔ 1 – 2m < 0 ⇔ 2m > 1 ⇔ m >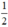 
+ Có nghiệm kép ⇔ Δ’ = 0 ⇔ 1 – 2m = 0 ⇔ m =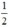 
+ Có hai nghiệm phân biệt ⇔ Δ’ > 0 ⇔ 1 – 2m > 0 ⇔ 2m < 1 ⇔ m <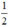 
Vậy: Phương trình (1) có hai nghiệm phân biệt khi m <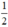 
; có nghiệm kép khi m = 
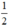và vô nghiệm khi m >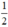 
Xét phương trình bậc hai ax2 + bx + c = 0 (a ≠ 0)
với b = 2b’ và biệt thức Δ ' = b ' 2 − a c
Trường hợp 1: Nếu ∆ < 0 thì phương trình vô nghiệm
Trường hợp 2: Nếu ∆ = 0 thì phương trình có nghiệm kép x1 = x2 = − b ' a
Trường hợp 3: nếu ∆ > 0 thì phương trình có hai nghiệm phân biệt
x1,2 = − b ' ± Δ ' a
Đáp án cần chọn là: A
a) 2 x 2 – 17 x + 1 = 0
Có a = 2; b = -17; c = 1
Δ = b 2 – 4 a c = ( - 17 ) 2 – 4 . 2 . 1 = 281 > 0 .
Theo hệ thức Vi-et: phương trình có hai nghiệm x1; x2 thỏa mãn:
x 1 + x 2 = − b / a = 17 / 2 x 1 x 2 = c / a = 1 / 2
b) 5 x 2 – x – 35 = 0
Có a = 5 ; b = -1 ; c = -35 ;
Δ = b 2 – 4 a c = ( - 1 ) 2 – 4 . 5 . ( - 35 ) = 701 > 0
Theo hệ thức Vi-et, phương trình có hai nghiệm x1; x2 thỏa mãn:
x 1 + x 2 = − b / a = 1 / 5 x 1 ⋅ x 2 = c / a = − 35 / 5 = − 7
c) 8 x 2 – x + 1 = 0
Có a = 8 ; b = -1 ; c = 1
Δ = b 2 – 4 a c = ( - 1 ) 2 – 4 . 8 . 1 = - 31 < 0
Phương trình vô nghiệm nên không tồn tại x1 ; x2.
d) 25 x 2 + 10 x + 1 = 0
Có a = 25 ; b = 10 ; c = 1
Δ = b 2 – 4 a c = 10 2 – 4 . 25 . 1 = 0
Khi đó theo hệ thức Vi-et có:
x 1 + x 2 = − b / a = − 10 / 25 = − 2 / 5 x 1 x 2 = c / a = 1 / 25
Đáp án C
Xét phương trình bậc hai a x 2 + b x + c = 0 ( a ≠ 0 ) có biệt thức b = 2b'; Δ ' = b ' 2 - a c :
Nếu Δ' = 0 thì phương trình có nghiệm kép
x
1
=
x
2
= 
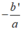
Xét phương trình bậc hai ax2 + bx + c = 0 (a ≠ 0)
có b = 2b’và biệt thức Δ ' = b ' 2 − a c
Nếu Δ ' =0 thì phương trình có nghiệm kép = − b a
Đáp án cần chọn là: C
Đáp án A
Xét phương trình bậc hai a x 2 + b x + c = 0 ( a ≠ 0 ) có biệt thức b = 2b'; Δ ' = b ' 2 - a c :
• TH1: Nếu Δ' < 0 thì phương trình vô nghiệm
• TH2: Nếu Δ' = 0 thì phương trình có nghiệm kép
x
1
=
x
2
= 
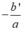
• TH3: Nếu Δ' > 0 thì phương trình có hai nghiệm phân biệt
x
1
,
2
= 
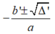
Xét phương trình bậc hai ax2 + bx + c = 0 (a ≠ 0)
với b = 2b’ và biệt thức Δ ' = b ' 2 − a c
Trường hợp 1: Nếu Δ ' < 0 thì phương trình vô nghiệm
Trường hợp 2: Nếu Δ ' = 0 thì phương trình có nghiệm kép x1 = x2 = − b ' a
Trường hợp 3: nếu Δ ' > 0 thì phương trình có hai nghiệm phân biệt
x1,2 = − b ' ± Δ ' a
Đáp án cần chọn là: D
Nếu Δ = 0 thì từ phương trình (2) suy ra (x + b/2a)2 =0
Do đó,phương trình (1) có nghiệm kép x = (-b)/2a
Xét phương trình bậc hai một ẩn
ax2 + bx + c = 0 (a ≠ 0) và biệt thức = b2 – 4ac
TH1: Nếu < 0 thì phương trình vô nghiệm
TH2. Nếu = 0 thì phương trình
có nghiệm kép x1 = x2 = − b 2 a
TH3: Nếu > 0 thì phương trình
có hai nghiệm phân biệt x1, 2 = − b ± Δ 2 a
Đáp án cần chọn là: C