Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ptr có nghiệm `<=>\Delta' >= 0`
`<=>[-(m+1)]^2-(m^2+4) >= 0`
`<=>m^2+2m+1-m^2-4 >= 0`
`<=>m >= 3/2`
Với `m >= 3/2`, áp dụng Vi-ét có:`{(x_1+x_2=[-b]/a=2m+2),(x_1.x_2=c/a=m^2+4):}`
Ta có:`C=x_1+x_2-x_1.x_2+3`
`<=>C=2m+2-m^2-4+3`
`<=>C=-m^2+2m+1`
`<=>C=-(m^2-2m+1)+2`
`<=>C=-(m-1)^2+2`
Vì `-(m-1)^2 <= 0 AA m >= 3/2`
`<=>-(m-1)^2+2 <= 2 AA m >= 3/2`
Dấu "`=`" xảy ra`<=>(m-1)^2=0<=>m=1` (ko t/m)
Vậy không tồn tại `m` để `C` có `GTLN`

a: \(\Delta=\left(2m+2\right)^2-4\left(m^2-2m-3\right)\)
\(=4m^2+8m+4-4m^2+8m+12\)
=16m+16
Để phương trình luôn có nghiệm thì 16m+16>=0
hay m>=-1
b: Theo đề, ta có: \(\left(x_1+x_2\right)^2-2x_1x_2-x_1x_2=28\)
\(\Leftrightarrow\left(2m+2\right)^2-3\left(m^2-2m-3\right)=28\)
\(\Leftrightarrow4m^2+8m+4-3m^2+6m+9=28\)
\(\Leftrightarrow m^2+14m-15=0\)
=>(m+15)(m-1)=0
=>m=1

a, Với m= 2, ta có 2 x 2 − 4 x + 2 = 0 ⇔ x = 1
b) Phương trình (1) có hai nghiệm x 1 , x 2 khi và chỉ khi Δ ' ≥ 0 ⇔ − 2 ≤ m ≤ 2
Theo Vi-et , ta có: x 1 + x 2 = m 1 x 1 . x 2 = m 2 − 2 2 2
Theo đề bài ta có: A = 2 x 1 x 2 − x 1 − x 2 − 4 = m 2 − 2 − m − 4 = m − 3 m + 2
Do − 2 ≤ m ≤ 2 nên m + 2 ≥ 0 , m − 3 ≤ 0 . Suy ra A = m + 2 − m + 3 = − m 2 + m + 6 = − m − 1 2 2 + 25 4 ≤ 25 4
Vậy MaxA = 25 4 khi m = 1 2 .

\(\Delta=1-4\left(-m-2\right)\ge0\Leftrightarrow m\ge-\dfrac{9}{4}\)
Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=-1\\x_1x_2=-m-2\end{matrix}\right.\)
\(x_1^2-x_1x_2-2x_2=16\)
\(\Leftrightarrow x_1\left(x_1+x_2\right)-2x_1x_2-2x_2=16\)
\(\Leftrightarrow-x_1-2\left(-m-2\right)-2x_2=16\)
\(\Leftrightarrow x_1+2x_2=2m-12\)
\(\Rightarrow x_1+x_2+x_2=2m-12\)
\(\Leftrightarrow-1+x_2=2m-12\Rightarrow x_2=2m-11\Rightarrow x_1=-1-x_2=-2m+10\)
Lại có: \(x_1x_2=-m-2\)
\(\Rightarrow\left(-2m+10\right)\left(2m-11\right)=-m-2\)
\(\Leftrightarrow4m^2-43m+108=0\Rightarrow\left[{}\begin{matrix}m=4\\m=\dfrac{27}{4}\end{matrix}\right.\)

a) Thay x=0 vào phương trình, ta được:
\(4\cdot0^2-2\cdot\left(2m+3\right)\cdot0+m+1=0\)
\(\Leftrightarrow m+1=0\)
hay m=-1
Áp dụng hệ thức Vi-et, ta có:
\(x_1+x_2=\dfrac{2\left(2m+3\right)}{4}\)
\(\Leftrightarrow x_1=\dfrac{2\cdot\left(-2+3\right)}{4}=\dfrac{2}{4}=\dfrac{1}{2}\)
Vậy: Khi m=-1 và nghiệm còn lại là \(x=\dfrac{1}{2}\)

a, Thay m=0 vào pt ta có:
\(x^2-x+1=0\)
\(\Rightarrow\) pt vô nghiệm
b, Để pt có 2 nghiệm thì \(\Delta\ge0\)
\(\Leftrightarrow\left(-1\right)^2-4.1\left(m+1\right)\ge0\\ \Leftrightarrow1-4m-4\ge0\\ \Leftrightarrow-3-4m\ge0\\ \Leftrightarrow4m+3\le0\\ \Leftrightarrow m\le-\dfrac{3}{4}\)
Theo Vi-ét:\(\left\{{}\begin{matrix}x_1+x_2=1\\x_1x_2=m+1\end{matrix}\right.\)
\(x_1x_2\left(x_1x_2-2\right)=3\left(x_1+x_2\right)\\ \Leftrightarrow\left(x_1x_2\right)^2-2x_1x_2=3.1\\ \Leftrightarrow\left(m+1\right)^2-2\left(m+1\right)-3=0\\ \Leftrightarrow\left[{}\begin{matrix}m+1=3\\m+1=-1\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}m=2\left(ktm\right)\\m=-2\left(tm\right)\end{matrix}\right.\)

a: Δ=(2m-1)^2-4*(-m)
=4m^2-4m+1+4m=4m^2+1>0
=>Phương trình luôn có nghiệm
b: \(A=\left(x_1+x_2\right)^2-2x_1x_2-x_1x_2\)
\(=\left(2m-1\right)^2-3\left(-m\right)\)
=4m^2-4m+1+3m
=4m^2-m+1
=4(m^2-1/4m+1/4)
=4(m^2-2*m*1/8+1/64+15/64)
=4(m-1/8)^2+15/16>=15/16
Dấu = xảy ra khi m=1/8

a)Nếu m=0 thì pt\(\Rightarrow-x-2=0\Rightarrow x=-2\)
\(\Rightarrow\)Pt có nghiệm duy nhất
\(\Rightarrow m=0\left(loại\right)\)
Nếu \(m\ne0\) thì pt có hai nghiệm
\(\Leftrightarrow\Delta\ge0\Rightarrow\left(2m+1\right)^2-4\cdot m\cdot\left(m-2\right)\ge0\)
\(\Rightarrow4m^2+4m+1-4m^2+8m\ge0\)
\(\Rightarrow m\ge-\dfrac{1}{12}\) thì pt có hai nghiệm \(x_1,x_2\)
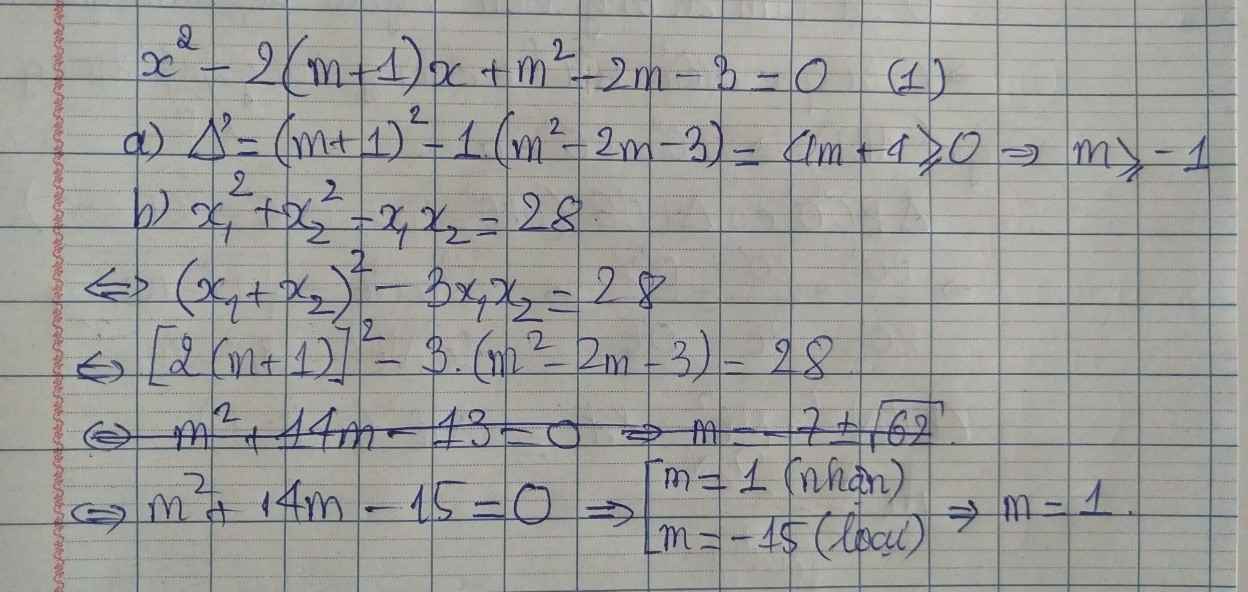
trời đất
ai tl hộ mình vs